Mezcla de dos cantidades de agua

De Laplace

(Diferencias entre revisiones)

Revisión de 22:38 10 mar 2013

1 Enunciado

En un recipiente aislado se ponen en contacto 750 cm³ de agua a 20 °C con 250 cm³ de agua a 80 °C. ¿Cuál es la temperatura final de la mezcla? ¿Cuánto calor ha pasado de un subsistema al otro?

¿Cuánta entropía se produce en el proceso?

2 Calor y temperatura

Tenemos un sistema aislado formado por las dos masas de agua. El único calor fluye de una parte del agua a la otra, pero no con el exterior. Si llamamos “1” al agua caliente originalmente y “2” a la fría, os queda la relación

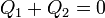
$Q_1 + Q_2=0\,$

o, dicho de otra forma

$Q_2 = -Q_1\,$

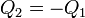
el calor que entra en el agua fría es igual al que sale de la caliente. Podemos escribir esto como

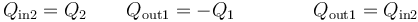
$Q_{\mathrm{in}2}=Q_2\qquad Q_{\mathrm{out}1} = -Q_1\qquad\qquad Q_{\mathrm{out}1}=Q_{\mathrm{in}2}$

Por otro lado, el calor que entra en el agua fría es proporcional a la diferencia de temperaturas entre la final y la inicial

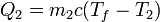
$Q_2 = m_2c(T_f-T_2)\,$

y el calor que entra en el agua caliente (que tendrá un valor negativo, porque en realidad sale) cumple la misma ley

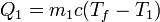
$Q_1 = m_1c(T_f-T_1)\,$

El calor específico del agua, $c$ , depende poco de la temperatura, por lo que podemos suponer el mismo valor para las dos masas de agua.

Llevando esto al calor neto

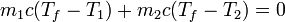
$m_1c(T_f-T_1)+m_2c(T_f-T_2)=0\,$

y despejando obtenemos la temperatura final

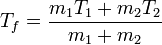
$T_f = \frac{m_1T_1+m_2T_2}{m_1+m_2}$

Puesto que a este resultado se llega a partir de diferencias entre temperaturas es válido tanto para temperaturas expresadas en grados Celsius como en kelvins.

Para sustituir los valores numéricos observamos que se nos dan los volúmenes, no las masas. Sin embargo, puede suponerse que dentro del rango de temperaturas la densidad del agua permanece constante, por lo que

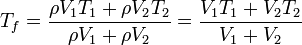
$T_f = \frac{\rho V_1 T_1+\rho V_2 T_2}{\rho V_1+\rho V_2} = \frac{V_1T_1+V_2 T_2}{V_1+V_2}$

es decir, también se trata de la media ponderada respecto a los volúmenes. 3/4 l de agua cuentan el triple que 1/4 l. Sustituyendo los valores numéricos en grados Celsius

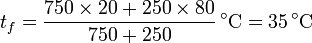
$t_f= \frac{750\times 20 + 250\times 80}{750+250}\,^\circ\mathrm{C}= 35\,^\circ\mathrm{C}$

La cantidad de calor que va del agua caliente a la fría es

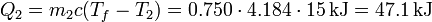
$Q_2 = m_2c(T_f-T_2) = 0.750\cdot 4.184\cdot 15\,\mathrm{kJ} = 47.1\,\mathrm{kJ}$

3 Producción de entropía

Para hallar la variación de la entropía del sistema debemos considerar un proceso reversible que lleve del estado inicial al final para cada una de las dos masas de agua.

La forma de hacerlo es considerar cada parte por separado y suponer que el calor que entra en cada una no procede de la otra, sino de una serie de focos térmicos situados a las temperaturas intermedias, de forma que imaginamos que el agua fría se va calentando gradualmente porque van entrando cantidades diferenciales de calor, de forma que la variación en su entropía es

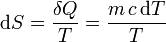
$\mathrm{d}S= \frac{\delta Q}{T}= \frac{m\,c\,\mathrm{d}T}{T}$

E integrando esta expresión

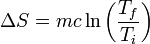
$\Delta S = mc\ln\left(\frac{T_f}{T_i}\right)$

Esto nos da, para el agua fría

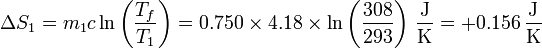
$\Delta S_1 = m_1c\ln\left(\frac{T_f}{T_1}\right) = 0.750\times 4.18\times\ln\left(\frac{308}{293}\right)\,\frac{\mathrm{J}}{\mathrm{K}}=+0.156\,\frac{\mathrm{J}}{\mathrm{K}}$

y para el agua caliente

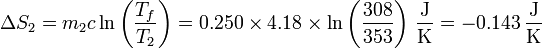
$\Delta S_2 = m_2c\ln\left(\frac{T_f}{T_2}\right) = 0.250\times 4.18\times\ln\left(\frac{308}{353}\right)\,\frac{\mathrm{J}}{\mathrm{K}}=-0.143\,\frac{\mathrm{J}}{\mathrm{K}}$

siendo la producción total de entropía

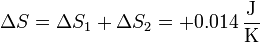
$\Delta S = \Delta S_1+\Delta S_2=+0.014\,\frac{\mathrm{J}}{\mathrm{K}}$

Esta cantidad es positiva, como corresponde a un proceso posible.

Mezcla de dos cantidades de agua

De Laplace

Revisión de 22:38 10 mar 2013

1 Enunciado

2 Calor y temperatura

3 Producción de entropía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

@@ Línea 12: / Línea 12: @@
 <center><math>Q_2 = -Q_1\,</math></center>
-el calor que entra en el agua fría es igual al que sale de la caliente.
+el calor que entra en el agua fría es igual al que sale de la caliente. Podemos escribir esto como
+<center><math>Q_{\mathrm{in}2}=Q_2\qquad Q_{\mathrm{out}1} = -Q_1\qquad\qquad Q_{\mathrm{out}1}=Q_{\mathrm{in}2}</math></center>
 Por otro lado, el calor que entra en el agua fría es proporcional a la diferencia de temperaturas entre la final y la inicial