Disipación de energía en un plano inclinado
De Laplace
(→Caso sin rozamiento) |
(→Caso sin rozamiento) |
||
| Línea 37: | Línea 37: | ||
Sustituyendo los datos numéricos | Sustituyendo los datos numéricos | ||
| - | <center><math>v_f = \sqrt{2\times 9.81\times 1.20}\frac{\mathrm{m}{s} = 4.85\,\frac{m}{s}</math></center> | + | <center><math>v_f = \sqrt{2\times 9.81\times 1.20}\frac{\mathrm{m}}{\mathrm{s}} = 4.85\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> |
Después de impactar, el muelle se comprime, almacenando esta energía mecánica, en forma de energía potencial elástica (sería un sistema KERS elemental). Cuando la masa rebota en el muelle la energía se recupera como energía cinética de nuevo, pero ahora la velocidad va en sentido contrario y la masa asciende por el plano. | Después de impactar, el muelle se comprime, almacenando esta energía mecánica, en forma de energía potencial elástica (sería un sistema KERS elemental). Cuando la masa rebota en el muelle la energía se recupera como energía cinética de nuevo, pero ahora la velocidad va en sentido contrario y la masa asciende por el plano. | ||
Revisión de 23:59 22 ene 2013
Contenido |
1 Enunciado
Un bloque de 500 g se encuentra en lo alto de un plano inclinado de 120 cm de altura y una pendiente del 75%. En el extremo inferior del plano se encuentra un resorte que hace rebotar a la masa elásticamente (sale con la misma rapidez con la que llega). Se suelta la masa, dejándola deslizarse por el plano.
- Suponga que no hay rozamiento entre la masa y el plano. ¿Con qué rapidez llega al punto más bajo? ¿Hasta que altura vuelve a subir tras rebotar en el resorte?
- Suponga ahora un coeficiente de rozamiento (estático y dinámico) μ = 0.25
- ¿Cuál es la rapidez al llegar al punto más bajo del plano?
- ¿Cuánta energía se ha disipado en el descenso?
- ¿Hasta que altura vuelve a ascender tras el rebote? ¿Cuánta energía se disipa en el ascenso?
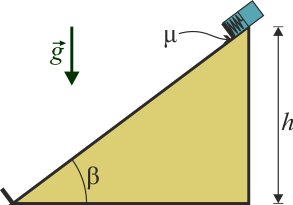
2 Caso sin rozamiento
En el caso de que no haya rozamiento, el bloque está sometido a dos fuerzas:
- El peso
- La reacción normal del plano.
La reacción normal no realiza trabajo, por ser ortogonal a la velocidad del bloque. La única fuerza que realiza trabajo es el peso, que se trata de una fuerza conservativa. Por tanto, en ausencia de rozamiento la energía mecánica se conserva. Lo que se pierde en energía cinética se gana en energía potencial
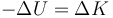
o, pasando todo al primer miembro

La expresión para la energía potencial es
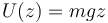
donde medimos z desde un cierto nivel de referencia, que puede ser el punto más bajo del plano. Nótese que aquí z es la distancia medida en la vertical, no a lo largo del plano. Nos queda entonces
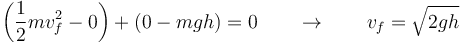
Es la misma expresión que resulta si la partícula cae verticalmente. La velocidad con la que llega abajo es independiente de la inclinación del plano y de la longitud de éste.
Sustituyendo los datos numéricos
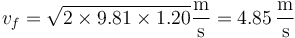
Después de impactar, el muelle se comprime, almacenando esta energía mecánica, en forma de energía potencial elástica (sería un sistema KERS elemental). Cuando la masa rebota en el muelle la energía se recupera como energía cinética de nuevo, pero ahora la velocidad va en sentido contrario y la masa asciende por el plano.
Puesto que la energía mecánica se conserva, toda esta energía vuelve a convertirse en energía potencial y la altura final vuelve a ser la de partida, 1.20\,m.





