Disipación de energía en un plano inclinado

De Laplace

Contenido

1 Enunciado
2 Caso sin rozamiento
3 Caso con rozamiento

1 Enunciado

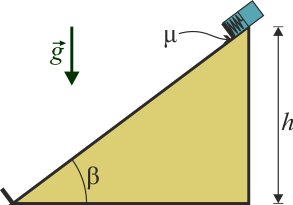
Un bloque de 500 g se encuentra en lo alto de un plano inclinado de 120 cm de altura y una pendiente del 75%. En el extremo inferior del plano se encuentra un resorte que hace rebotar a la masa elásticamente (sale con la misma rapidez con la que llega). Se suelta la masa, dejándola deslizarse por el plano.

Suponga que no hay rozamiento entre la masa y el plano. ¿Con qué rapidez llega al punto más bajo? ¿Hasta que altura vuelve a subir tras rebotar en el resorte?
Suponga ahora un coeficiente de rozamiento (estático y dinámico) μ = 0.25
1. ¿Cuál es la rapidez al llegar al punto más bajo del plano?
2. ¿Cuánta energía se ha disipado en el descenso?
3. ¿Hasta que altura vuelve a ascender tras el rebote? ¿Cuánta energía se disipa en el ascenso?

2 Caso sin rozamiento

En el caso de que no haya rozamiento, el bloque está sometido a dos fuerzas:

El peso
La reacción normal del plano.

La reacción normal no realiza trabajo, por ser ortogonal a la velocidad del bloque. La única fuerza que realiza trabajo es el peso, que se trata de una fuerza conservativa. Por tanto, en ausencia de rozamiento la energía mecánica se conserva. Lo que se pierde en energía cinética se gana en energía potencial

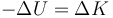
$-\Delta U = \Delta K\,$

o, pasando todo al primer miembro

$\Delta E = \Delta K + \Delta U = 0\,$

La expresión para la energía potencial es

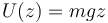
$U(z) = mgz\,$

donde medimos $z$ desde un cierto nivel de referencia, que puede ser el punto más bajo del plano. Nótese que aquí $z$ es la distancia medida en la vertical, no a lo largo del plano. Nos queda entonces

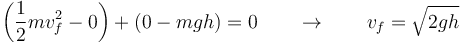
$\left(\frac{1}{2}mv_f^2-0\right)+(0-mgh) = 0 \qquad\rightarrow\qquad v_f = \sqrt{2gh}$

Es la misma expresión que resulta si la partícula cae verticalmente. La velocidad con la que llega abajo es independiente de la inclinación del plano y de la longitud de éste.

Sustituyendo los datos numéricos

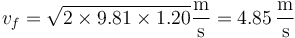
$v_f = \sqrt{2\times 9.81\times 1.20}\frac{\mathrm{m}}{\mathrm{s}} = 4.85\,\frac{\mathrm{m}}{\mathrm{s}}$

El valor de la energía mecánica en todo el proceso es

$E = mgh = 0.5\times 9.81\times 1.20\,\mathrm{J} = 5.89\,\mathrm{J}$

Después de impactar, el muelle se comprime, almacenando esta energía mecánica, en forma de energía potencial elástica (sería un sistema KERS elemental). Cuando la masa rebota en el muelle la energía se recupera como energía cinética de nuevo, pero ahora la velocidad va en sentido contrario y la masa asciende por el plano.

Puesto que la energía mecánica se conserva, toda esta energía vuelve a convertirse en energía potencial y la altura final vuelve a ser la de partida, 1.20 m.

3 Caso con rozamiento

Cuando hay rozamiento, aparece una nueva fuerza que se opone al movimiento. Esta fuerza es tangente al plano y, por tratarse de un rozamiento dinámico cumple

$|\vec{F}_r| = \mu|\vec{F}_n|$

Puesto que la fuerza normal compensa la componente normal del peso, su valor (como se ve en otro problema) es, en módulo

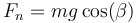
$F_n = mg\cos(\beta)\,$

siendo $β$ el ángulo de inclinación del plano. El dato que se ns da es la pendiente, que se relaciona con el ángulo por

$\mathrm{tg}(\beta) = 0.75=\frac{3}{4}\qquad\Rightarrow\qquad \cos(\beta) = 0.80=\frac{4}{5}\qquad\qquad \mathrm{sen}(\beta) = 0.60=\frac{3}{5}$

Esto nos da la fuerza de rozamiento

$F_r = \mu m g\cos(\beta)\,$

siendo su sentido el opuesto al movimiento, es decir, apunta hacia arriba cuando la masa desciende, y hacia abajo cuando asciende.

3.1 Rapidez

La acción combinada de esta fuerza y el peso producen un movimiento uniformemente acelerado. A partir de las ecuaciones de este movimiento puede hallarse la rapidez en el momento del impacto. No obstante, podemos hallarla también empleando métodos energéticos.

En presencia de rozamiento la energía mecánica no se conserva, ya que se va disipando por fricción. La ley para la energía se escribe entonces

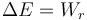
$\Delta E = W_r\,$

siendo $W r$ el trabajo realizado por la fuerza de rozamiento. Puesta que esta fuerza es constante y opuesta al movimiento, el trabajo es simplemente

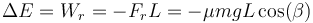
$\Delta E = W_r=-F_rL = -\mu m g L \cos(\beta)\,$

siendo L la longitud del plano. Por simple trigonometría

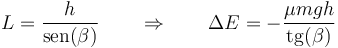
$L = \frac{h}{\mathrm{sen}(\beta)}\qquad\Rightarrow\qquad \Delta E = -\frac{\mu m g h}{\mathrm{tg}(\beta)}$

Sustituyendo, como antes, las expresiones de la energía cinética y la potencial

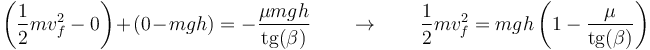
$\left(\frac{1}{2}mv_f^2-0\right)+(0-mgh) = -\frac{\mu m g h}{\mathrm{tg}(\beta)} \qquad\rightarrow\qquad \frac{1}{2}mv_f^2 = mgh\left(1-\frac{\mu}{\mathrm{tg}(\beta)}\right)$

Despejamos la rapidez

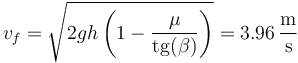
$v_f = \sqrt{2gh\left(1-\frac{\mu}{\mathrm{tg}(\beta)}\right)} = 3.96\,\frac{\mathrm{m}}{\mathrm{s}}$

3.2 Energía disipada

La cantidad de energía perdida en el proceso vale

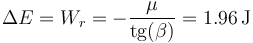
$\Delta E = W_r = -\frac{\mu}{\mathrm{tg}(\beta)}=1.96\,\mathrm{J}$

con lo cual, cuando llega abajo, la masa tiene solamente

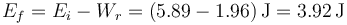
$E_f = E_i-W_r = (5.89-1.96)\,\mathrm{J} = 3.92\,\mathrm{J}$

En proporción, se ha perdido

$\frac{|\Delta E|}{E_i}=\frac{1.96}{5.89} = 33.3\%$

es decir, 1/3 de la energía inicial

3.3 Altura máxima

La masa rebota en el muelle de forma elástica y vuelve a ascender. En la subida, la fuerza de rozamiento vuelve a frenar a la masa, yendo ahora esta fuerza dirigida hacia abajo. Puesto que ahora el desplazamiento es hacia arriba, esto implica que el trabajo de rozamiento es de nuevo negativo. El teorema de la energía mecánica se escribe ahora

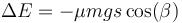
$\Delta E = -\mu m g s\cos(\beta)\,$

siendo $s$ la distancia recorrida por la masa en su ascenso hasta que se para. Aun no conocemos el valor de esta distancia, pero sí que se relaciona con la altura $z$ de subida por

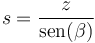
$s = \frac{z}{\mathrm{sen}(\beta)}$

Sustituyendo la energía cinética y la potencial

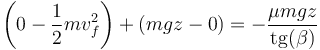
$\left(0-\frac{1}{2}mv_f^2\right)+(mgz-0) = -\frac{\mu m g z}{\mathrm{tg}(\beta)}$

Obsérvese que ahora la energía cinética final es nula y la inicial es la que es distinta de cero y al contrario ocurre con la potencial. Despejando de aquí z.

$z = \frac{v_f^2}{2g(1+\mu/\mathrm{tg}(\beta))}$

y sustituyendo el valor de la rapidez que calculamos en el apartado anterior

$z = h\frac{1-\mu/\mathrm{tg}(\beta)}{1+\mu/\mathrm{tg}(\beta)}$

Podemos obtener una solución racional sustituyendo los decimales por fracciones

$\mu = 0.25 = \frac{1}{4}\qquad \qquad\mathrm{tg}(\beta)= 0.75 = \frac{3}{4}$

y queda

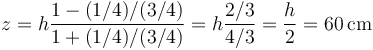
$z = h\frac{1-(1/4)/(3/4)}{1+(1/4)/(3/4)} = h\frac{2/3}{4/3}=\frac{h}{2} = 60\,\mathrm{cm}$

También podemos hallarla simplemente sustituyendo los resultados ya conocidos

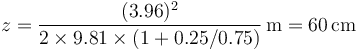
$z = \frac{(3.96)^2}{2\times 9.81\times(1+0.25/0.75)}\,\mathrm{m}=60\,\mathrm{cm}$

La energía disipada en la subida no es toda la energía, aunque al final se pare, ya que parte queda almacenada como energía potencial. La cantidad de energía que se disipa es

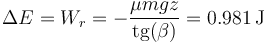
$\Delta E = W_r = -\frac{\mu m g z}{\mathrm{tg}(\beta)} = 0.981\,\mathrm{J}$

Esta energía es la mitad que antes, pues ha subido hasta medio plano y el trabajo realizado por la fuerza de rozamiento es la mitad. En proporción, la pérdida de energía respecto a la que tiene al iniciar el ascenso es

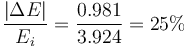
$\frac{|\Delta E|}{E_i} =\frac{0.981}{3.924} = 25\%$

es decir, se pierde 1/4 de la que tuviera al empezar a subir. Puesto que esta era 2/3 de la que tenía al empezar a bajar, en la subida pierde 1/6 de la inicial del todo. En total, sumando la bajada y la subida, se pierde 1/2 de la energía inicial.

3.4 Rebotes sucesivos

En este sistema, el proceso continúa con rebotes cada vez más pequeños.

La cantidad de energía disipada en la bajada es 1/3 de la que tuviera cuando empieza cada descenso, y 1/6 la disipada en la subida, siendo 1/2 la disipada en el proceso completo. Esto quiere decir que en cada rebote la energía se reduce a la mitad.
Por ello, la siguiente vez subirá solo hasta 1/4 de la altura, más adelante hasta 1/8, 1/16, etc.
En cuanto a la velocidad de impacto, disminuye como la 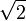$\sqrt{2}$ en cada oscilación.

Disipación de energía en un plano inclinado

De Laplace

Contenido

1 Enunciado

2 Caso sin rozamiento

3 Caso con rozamiento

3.1 Rapidez

3.2 Energía disipada

3.3 Altura máxima

3.4 Rebotes sucesivos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES