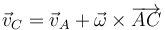Propiedades de un sistema de 8 partículas
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Para los movimientos compatibles del problema “Clasificación de movimientos de un sólido” calcule la cantidad de movimiento, el momento cinético…') |
|||
| Línea 5: | Línea 5: | ||
==Introducción== | ==Introducción== | ||
| - | Este problema combina la solución de otros dos problemas. Por un lado, en “[[Clasificación de movimientos de un sólido]]” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en | + | Este problema combina la solución de otros dos problemas. Por un lado, en “[[Clasificación de movimientos de un sólido]]” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en “[[Momento de inercia de un sistema de partículas]]”, se halla el momento de inercia de un sistema de ocho partículas como el que se emplea en este problema. |
| + | |||
| + | La técnica general en lo que sigue es: | ||
| + | |||
| + | ;Cantidad de movimiento: Para un sistema de partículas se cumple | ||
| + | |||
| + | <center><math>\vec{p}=M\vec{v}_C</math></center> | ||
| + | |||
| + | :donde <math>M</math> es la masa total del sistema y <math>\vec{v}_C</math> la velocidad de su centro de masas, la cual se puede calcular como la de un punto más del sólido | ||
| + | |||
| + | <center><math>\vec{v}_C=\vec{v}_A+\vec{\omega}\times\overrightarrow{AC}</math></center> | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 11:48 15 ene 2013
1 Enunciado
Para los movimientos compatibles del problema “Clasificación de movimientos de un sólido” calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.
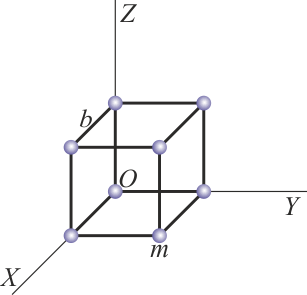
2 Introducción
Este problema combina la solución de otros dos problemas. Por un lado, en “Clasificación de movimientos de un sólido” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en “Momento de inercia de un sistema de partículas”, se halla el momento de inercia de un sistema de ocho partículas como el que se emplea en este problema.
La técnica general en lo que sigue es:
- Cantidad de movimiento
- Para un sistema de partículas se cumple
- donde M es la masa total del sistema y
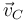la velocidad de su centro de masas, la cual se puede calcular como la de un punto más del sólido
