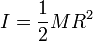Entrar Página Discusión Historial Go to the site toolbox

Momento de inercia de sólidos cilíndricos

De Laplace

(Diferencias entre revisiones)
(→Cilindro macizo)
(→Cilindro macizo)
Línea 44: Línea 44:
Esto nos da el diferencial de masa
Esto nos da el diferencial de masa
-
<center><math>\mathrm{d}M=\rho\,\mathrm{d}V=\frac{M}{\pi R^2H}(2\pi\,r\,H\,\mathrm{d}r = \frac{2M\,r\,\mathrm{d}r}{R^2}</math></center>
+
<center><math>\mathrm{d}M=\rho\,\mathrm{d}V=\frac{M}{\pi R^2H}(2\pi\,r\,H\,\mathrm{d}r) = \frac{2M\,r\,\mathrm{d}r}{R^2}</math></center>
el de momento de inercia
el de momento de inercia

Revisión de 20:14 5 ene 2013

Contenido

1 Enunciado

Halle los siguientes momentos de inercia de sólidos de densidad homogénea:

  1. Una superficie cilíndrica hueca, de masa M, radio R y altura H.
  2. Un cilindro macizo, de masa M, radio R y altura H.
  3. Una corona cilíndrica de masa M, radio interior R1 y exterior R2, con altura H

En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro.

2 Superficie cilíndrica

El momento de inercia de un sólido respecto a un eje se define como la cantidad

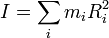
I = \sum_i m_i R_i^2\,

donde Ri es la distancia de la masa mi respecto al eje en cuestión. En el caso de una distribución continua, la suma se transforma en la integral correspondiente

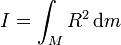
I = \int_M R^2\,\mathrm{d}m

En el caso de una superficie cilíndrica de radio R, todos los puntos se hallan a la misma distancia del eje, por lo que R es una constante y puede salir de la integral, quedando simplemente

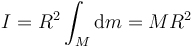
I = R^2\int_M\mathrm{d}m = M R^2\,

3 Cilindro macizo

En un cilindro macizo no todos los puntos se encuentran a la misma distancia del eje. Podemos agruparlos en coronas cilíndricas de radios crecientes.

Si r es el radio de una de las capas, su momento de inercia diferencial será el de una superficie cilíndrica

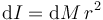
\mathrm{d}I = \mathrm{d}M\,r^2

El diferencial de masa depende del radio que se tome. Cuanto mayor sea r, mayor será la masa, por lo que debe tenerse en cuenta a la hora de integrar. La masa de cada capa será el producto de la densidad por el volumen

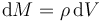
\mathrm{d}M = \rho\,\mathrm{d}V

La densidad de masa, por tratarse de un sólido homogéneo, es igual a la masa total dividida por el volumen total

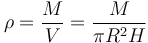
\rho=\frac{M}{V}=\frac{M}{\pi R^2 H}

mientras que el diferencial de volumen es el de una fina capa de radio r, espesor dr y altura H. Este volumen es el producto del área por el espesor

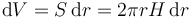
\mathrm{d}V = S\,\mathrm{d}r = 2\pi r H\,\mathrm{d}r

Esto nos da el diferencial de masa

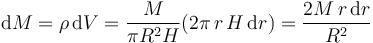
\mathrm{d}M=\rho\,\mathrm{d}V=\frac{M}{\pi R^2H}(2\pi\,r\,H\,\mathrm{d}r) = \frac{2M\,r\,\mathrm{d}r}{R^2}

el de momento de inercia

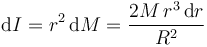
\mathrm{d}I =r^2\,\mathrm{d}M=\frac{2M\,r^3\,\mathrm{d}r}{R^2}

y el momento de inercia total

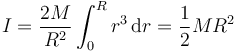
I = \frac{2M}{R^2}\int_0^R r^3\,\mathrm{d}r = \frac{1}{2}MR^2

Vemos que a igualdad de masa y de radio, el momento de inercia del cilindro macizo es la mitad que el de la superficie cilíndrica, por estar la masa más concentrada.

4 Corona cilíndrica

4.1 Por integración

Dividimos la corona cilíndrica en finas capas concéntricas, de radio r y espesor dr. El volumen diferencial de cada una de estas capas es

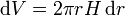
\mathrm{d}V = 2\pi r H\,\mathrm{d}r

mientras que la distancia al eje de los puntos de cada capa es r. Esto nos da la integral para el momento de inercia

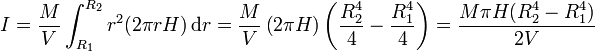
I = \frac{M}{V}\int_{R_1}^{R_2} r^2(2\pi r H)\,\mathrm{d}r=\frac{M}{V}\left(2\pi H\right)\left(\frac{R_2^4}{4}-\frac{R_1^4}{4}\right) = \frac{M \pi H (R_2^4-R_1^4)}{2V}

El volumen total de esta corona es

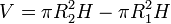
V = \pi R_2^2 H - \pi R_1^2H\,

lo que nos da el momento de inercial

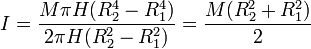
I = \frac{M\pi H(R_2^4-R_1^4)}{2\pi H (R_2^2-R_1^2)} = \frac{M(R_2^2+R_1^2)}{2}

Como caso particular de este resultado tenemos:

Superficie cilíndrica
Tiene R1 = R2 = R y queda
I = MR^2\,
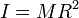
Anillo circular
Es un caso particular del anterior, pues el resultado no depende de la altura del cilindro
I = MR^2\,
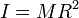
Cilindro macizo
Hacemos R1 = 0, R2 = R y resulta
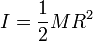
I = \frac{1}{2}MR^2\,
Disco circular
Es un caso particular del anterior
I = \frac{1}{2}MR^2\,

4.2 Por superposición

Obtenido de "http://tesla.us.es/wiki/index.php/Momento_de_inercia_de_s%C3%B3lidos_cil%C3%ADndricos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace