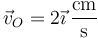Ejemplo gráfico de movimiento plano
De Laplace
(Diferencias entre revisiones)
(→Condición de rigidez) |
(→Condición de rigidez) |
||
| Línea 24: | Línea 24: | ||
donde | donde | ||
| - | <center><math>\overrightarrow{OA}=\vec{r}_A-\vec{r}_O=(4\vec{\jmath})\,\mathrm{cm}\qquad\qquad\vec{v}_A=-2\,\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | + | <center><math>\overrightarrow{OA}=\vec{r}_A-\vec{r}_O=(4\vec{\jmath})\,\mathrm{cm}\qquad\qquad\vec{v}_A=(-2\,\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}</math></center> |
lo que nos da una componente de la velocidad del origen | lo que nos da una componente de la velocidad del origen | ||
<center><math>\left\{\begin{array}{rcl}\vec{v}_O\cdot\overrightarrow{OA}&=&(v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath})\cdot(4\vec{\jmath})= 4v_{Oy} \\ \vec{v}_A\cdot\overrightarrow{OA}&=&(-2\,\vec{\imath})\cdot(4\vec{\jmath})=0\end{array}\right.\qquad\Rightarrow\qquad v_{Oy}=0</math></center> | <center><math>\left\{\begin{array}{rcl}\vec{v}_O\cdot\overrightarrow{OA}&=&(v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath})\cdot(4\vec{\jmath})= 4v_{Oy} \\ \vec{v}_A\cdot\overrightarrow{OA}&=&(-2\,\vec{\imath})\cdot(4\vec{\jmath})=0\end{array}\right.\qquad\Rightarrow\qquad v_{Oy}=0</math></center> | ||
| + | |||
| + | De manera análoga, tenemos, para el punto B | ||
| + | |||
| + | <center><math>\overrightarrow{OB}=\vec{r}_A-\vec{r}_O=(4\vec{\imath})\,\mathrm{cm}\qquad\qquad\vec{v}_B=(2\,\vec{\imath}+4\vec{\jmath})\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcl}\vec{v}_O\cdot\overrightarrow{OB}&=&(v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath})\cdot(4\vec{\imath})= 4v_{Ox} \\ \vec{v}_B\cdot\overrightarrow{OB}&=&(2\,\vec{\imath}+4\vec{\jmath})\cdot(4\vec{\imath})=8\end{array}\right.\qquad\Rightarrow\qquad v_{Oy}=2</math></center> | ||
| + | |||
| + | Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial | ||
| + | |||
| + | <center><math>\vec{v}_O=2\vec{\imath}\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
==Centro instantáneo de rotación== | ==Centro instantáneo de rotación== | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
Revisión de 11:55 23 dic 2012
Contenido |
1 Enunciado
En un movimiento plano, se tiene que la velocidad instantánea de dos puntos A y B es la ilustrada en la figura (para la posición, la cuadrícula representa cm y para la velocidad cm/s)

- En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
- ¿Dónde se encuentra el centro instantáneo de rotación?
2 Velocidad del origen
Podemos hallar la velocidad del punto O:
- Aplicando la condición cinemática de rigidez
- Mediante la fórmula del campo de velocidades
- Gráfica o analíticamente una vez localizado el CIR
2.1 Condición de rigidez
La velocidad del origen la podemos escribir como
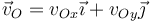
Esta velocidad debe cumplir, junto con la del punto A, la condición de rigidez o de equiproyectividad
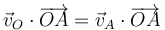
donde
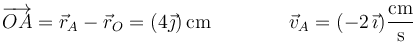
lo que nos da una componente de la velocidad del origen
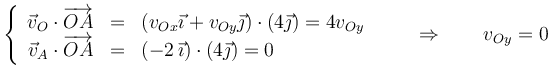
De manera análoga, tenemos, para el punto B
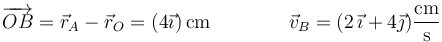
y
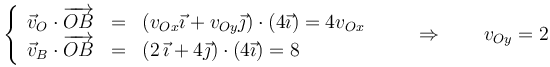
Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial