Fuerza entre un anillo y un dipolo
De Laplace
(→Par sobre el dipolo) |
(→Fuerza del dipolo sobre la espira) |
||
| Línea 20: | Línea 20: | ||
<center><math>\mathbf{E}_\mathrm{p} = \frac{3(\mathbf{p}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{p}}{4\pi\varepsilon_0 r^5} \qquad \mathbf{p} = p\mathbf{u}_{z}</math></center> | <center><math>\mathbf{E}_\mathrm{p} = \frac{3(\mathbf{p}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{p}}{4\pi\varepsilon_0 r^5} \qquad \mathbf{p} = p\mathbf{u}_{z}</math></center> | ||
| - | El campo debe evaluarse en los puntos del anillo. Empleando coordenadas cilíndricas | + | [[Imagen:dipoloespira.png|left]]El campo debe evaluarse en los puntos del anillo. Empleando coordenadas cilíndricas |
<center><math>\mathbf{r} = a\mathbf{u}_{\rho}</math>{{qquad}}<math>r = a</math>{{qquad}}<math>\mathbf{r}{\cdot}\mathbf{p} = 0</math>{{qquad}}<math>\mathbf{E}_\mathrm{p}(a\mathbf{u}_{\rho}) = -\frac{p\mathbf{u}_{z}}{4\pi\varepsilon_0 a^3}</math></center> | <center><math>\mathbf{r} = a\mathbf{u}_{\rho}</math>{{qquad}}<math>r = a</math>{{qquad}}<math>\mathbf{r}{\cdot}\mathbf{p} = 0</math>{{qquad}}<math>\mathbf{E}_\mathrm{p}(a\mathbf{u}_{\rho}) = -\frac{p\mathbf{u}_{z}}{4\pi\varepsilon_0 a^3}</math></center> | ||
última version al 12:52 6 nov 2008
Contenido |
1 Enunciado
Un anillo circular de radio a, almacena una carga Q distribuida uniformemente. En el centro del anillo se encuentra un dipolo puntual 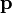 , alineado según el eje de la espira.
, alineado según el eje de la espira.
- Determine la fuerza que el dipolo ejerce sobre la espira.
- Halle la energía que tiene el dipolo por encontrarse en el campo de la espira.
- Calcule la fuerza que la espira produce sobre el dipolo. ¿Se verifica la tercera ley de Newton?
- Calcule el par que la espira ejerce sobre el dipolo.
2 Solución
2.1 Fuerza del dipolo sobre la espira
La fuerza sobre una distribución de carga lineal es
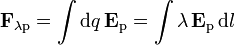
siendo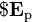 el campo externos en los puntos de la distribución. En este caso, este campo es el del dipolo situado en su centro.
el campo externos en los puntos de la distribución. En este caso, este campo es el del dipolo situado en su centro.
Situando el origen de coordenadas en el centro del anillo y el eje Z como el del anillo, el campo del dipolo es
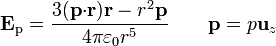
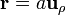 r = a
r = a 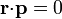
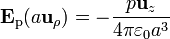
esto es, en todos los puntos del anillo, el campo del dipolo vale lo mismo. Esto es consecuencia de la simetría acimutal del campo de un dipolo.
La fuerza es entonces
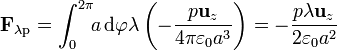
El anillo es empujado hacia abajo por el campo del dipolo, que en todos los puntos del anillo va en la dirección de 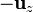
2.2 Energía potencial del dipolo
La energía del anillo por hallarse en el centro de la espira es
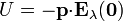
siendo 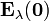 el campo del anillo en la posición del dipolo. Este valor lo obtenemos particularizando el campo de un anillo en los puntos de su eje (calculado en otro problema):
el campo del anillo en la posición del dipolo. Este valor lo obtenemos particularizando el campo de un anillo en los puntos de su eje (calculado en otro problema):
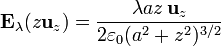
que en el centro se reduce a
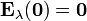
por lo que
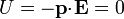
2.3 Fuerza de la espira sobre el dipolo
Para hallar la fuerza que el anillo ejerce sobre el dipolo aplicamos que
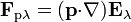
Para aplicar el operador 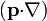 debemos poder derivar el campo creado por el anillo. Sin embargo, sólo conocemos la expresión del campo en los puntos de su eje (para todo z, con x = y = 0), indicada en el apartado anterior, por lo que podemos derivar respecto a z pero no respecto a x e y. Afortunadamente, esto es todo lo que necesitamos, ya que el dipolo se encuentra alineado con el eje (
debemos poder derivar el campo creado por el anillo. Sin embargo, sólo conocemos la expresión del campo en los puntos de su eje (para todo z, con x = y = 0), indicada en el apartado anterior, por lo que podemos derivar respecto a z pero no respecto a x e y. Afortunadamente, esto es todo lo que necesitamos, ya que el dipolo se encuentra alineado con el eje (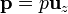 ), por
lo que
), por
lo que
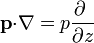
y la fuerza sobre el dipolo es

Derivando y sustituyendo $z$ por 0 (la posición del dipolo) queda
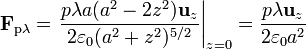
El dipolo es empujado hacia arriba por el campo del anillo. Podemos entender esto observando que la carga positiva del dipolo, que está ligeramente por encima del plano del anillo es repelida hacia arriba, mientras que la carga negativa, situada ligeramente por debajo, es atraída por el anillo (de nuevo hacia arriba).
Nótese que no hay contradicción alguna entre que la energía del dipolo sea nula, y que esté sometido a una cierta fuerza. Lo primero requiere el valor del campo en el centro mientras que lo segundo requiere su derivada en el mismo punto, por lo que se trata de cantidades independientes.
Como era de esperar resulta una fuerza que verifica la tercera ley de Newton respecto a la calculada en el apartado anterior
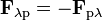
2.4 Par sobre el dipolo
El par que puede ejercer el anillo sobre el dipolo es
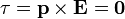
ya que, como hemos visto en el segundo apartado, el campo en el centro del anillo es nulo, por lo que el anillo no ejerce momento alguno sobre el dipolo.






