Guillotina que corta un papel
De Laplace
(→Introducción: representación en el sistema S) |
(→Introducción: representación en el sistema S) |
||
| Línea 29: | Línea 29: | ||
<center>[[Archivo:guillotina-04.png]]</center> | <center>[[Archivo:guillotina-04.png]]</center> | ||
| + | |||
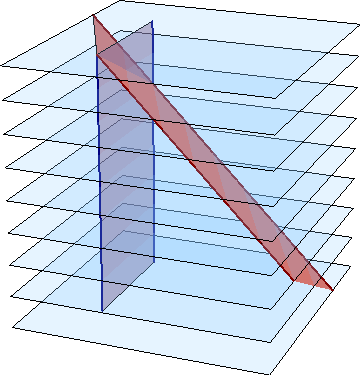
| + | Puesto que el tiempo es una variable continua, podemos unir las diferentes instantáneas. En esta representación el borde del papel se ve como un rectángulo vertical, mientras que el de la guillotina es uno oblicuo. | ||
| + | |||
| + | <center>[[Archivo:guillotina-04.png]]</center> | ||
| + | |||
| + | Finalmente, prescindimos de los planos horizontales que son las instantáneas y nos queda la intersección de dos polígonos | ||
| + | |||
| + | <center>[[Archivo:guillotina-05.png]]</center> | ||
==Transformación al sistema S'== | ==Transformación al sistema S'== | ||
Revisión de 12:19 10 nov 2012
Contenido |
1 Enunciado
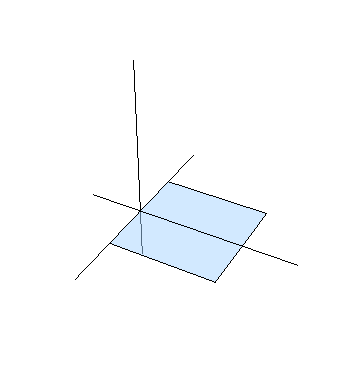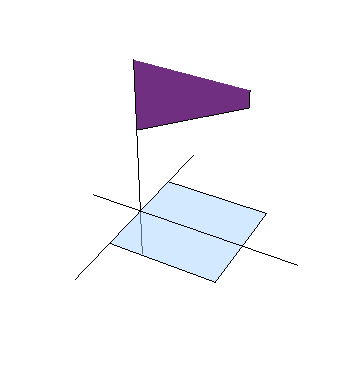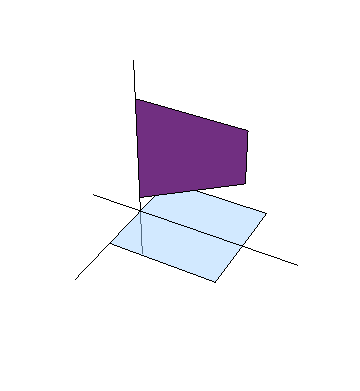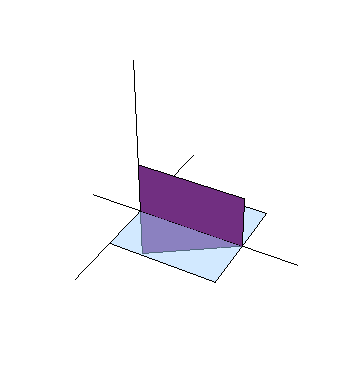
Supongamos una guillotina en el plano XZ (X el eje horizontal y Z el vertical). La guillotina tiene anchura L y un borde inferior rectilíneo con pendiente m. La guillotina desciende con velocidad constante u. En el plano XY se encuentra una hoja de papel horizontal, también de anchura L y situada justo debajo de la guillotina. La guillotina cae y corta el papel.
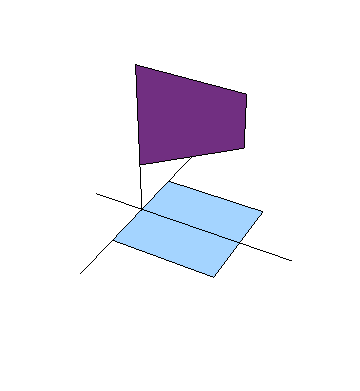
- Demuestre que para un observador S' que se mueva a lo largo del eje X con velocidad v, el borde de la guillotina puede verse inclinado hacia el lado contrario (esto es, con pendiente negativa).
- En el sistema en reposo respecto al papel, éste es cortado de izquierda a derecha (hacia X positivo). En el sistema S' del apartado anterior, ¿en qué sentido se produce el corte?
- Supongamos que cuando la guillotina ha cortado la mitad del papel se detiene bruscamente, interrumpiéndose el corte. ¿Qué se aprecia en ese caso en el sistema S'?
2 Introducción: representación en el sistema S
A la hora de representar este problema, pare que necesitamos las cuatro dimensiones del espaciotiempo, ya que tenemos X e Y (donde se encuentra el papel), Z (por donde baja la guillotina) y el tiempo, ya que se trata de un sistema en movimiento. Esto dificulta su representación gráfica.
Sin embargo, es fácil ver que podemos omitir una de las dimensiones espaciales. Al analizar la cinemática del problema, lo único que nos interesa es estudiar lo que ocurre con dos segmentos:
- El borde de la guillotina
- La línea del papel que es cortada
Todo lo demás es superfluo a la hora de resolver el problema.
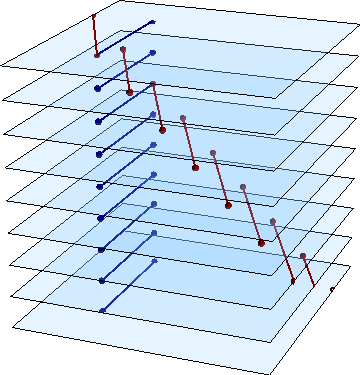
Gráficamente, para representar el movimiento de estos segmentos, podemos emplear una película

una superposición de fotogramas

o una representación tridimensional, siendo la tercera dimensión el tiempo. Para ello, apilamos los fotogramas
Puesto que el tiempo es una variable continua, podemos unir las diferentes instantáneas. En esta representación el borde del papel se ve como un rectángulo vertical, mientras que el de la guillotina es uno oblicuo.

Finalmente, prescindimos de los planos horizontales que son las instantáneas y nos queda la intersección de dos polígonos