Entrar Página Discusión Historial Go to the site toolbox

Cálculos a partir de magnitudes cinemáticas instantáneas

De Laplace

(Diferencias entre revisiones)
(→Aceleración tangencial)
(→Rapidez)
Línea 13: Línea 13:
Es el módulo de la velocidad
Es el módulo de la velocidad
-
<center><math>|\vec{v}|=\sqrt{4.00^2+3.00^2}\frac{\mathrm{m}}{\mathrm{s}} = 5.00\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>|\vec{v}|=\sqrt{0^2 +4.00^2+3.00^2}\frac{\mathrm{m}}{\mathrm{s}} = 5.00\frac{\mathrm{m}}{\mathrm{s}}</math></center>
==Componentes de la aceleración==
==Componentes de la aceleración==

Revisión de 09:31 23 oct 2012

Contenido

1 Enunciado

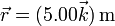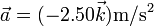En un instante dado, una partícula ocupa la posición \vec{r}=(5.00\vec{k})\,\mathrm{m}, tiene una velocidad \vec{v}=(4.00\vec{\jmath}+3.00\vec{k})\mathrm{m}/\mathrm{s} y una aceleración \vec{a}=(-2.50\vec{k})\mathrm{m}/\mathrm{s}^2. Para este instante, halle

  1. Su rapidez
  2. Su aceleración tangencial y su aceleración normal
  3. Los vectores tangente y normal a la trayectoria
  4. El radio de curvatura de la trayectoria
  5. El centro de curvatura
  6. ¿Cuál es su posición en m y su velocidad en m/s un tiempo 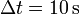\Delta t = 10\,\mathrm{s} más tarde?

2 Rapidez

Es el módulo de la velocidad

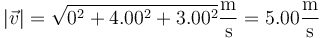
|\vec{v}|=\sqrt{0^2 +4.00^2+3.00^2}\frac{\mathrm{m}}{\mathrm{s}} = 5.00\frac{\mathrm{m}}{\mathrm{s}}

3 Componentes de la aceleración

3.1 Aceleración tangencial

No podemos hallar la aceleración tangencial como la derivada de la rapidez, ya que la conocemos en un solo instante. En su lugar, calculamos esta componente como la proyección sobre la velocidad. En forma escalar


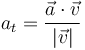
a_t = \frac{\vec{a}\cdot\vec{v}}{|\vec{v}|}

Siendo

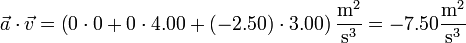
\vec{a}\cdot\vec{v}=\left(0\cdot 0+0\cdot 4.00+(-2.50)\cdot 3.00\right)\frac{\mathrm{m}^2}{\mathrm{s}^3}=-7.50\frac{\mathrm{m}^2}{\mathrm{s}^3}

obtenemos

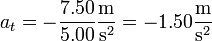
a_t = -\frac{7.50}{5.00}\frac{\mathrm{m}}{\mathrm{s}^2}=-1.50\frac{\mathrm{m}}{\mathrm{s}^2}

y en forma vectorial

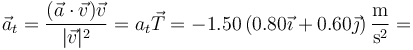
\vec{a}_t = \frac{(\vec{a}\cdot\vec{v})\vec{v}}{|\vec{v}|^2}=a_t\vec{T}=-1.50\left(0.80\vec{\imath}+0.60\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}^2}=

3.2 Aceleración normal

Podemos hallar la aceleración normal mediante la proyección ortogonal

a_n = \frac{|\vec{a}\times\vec{v}|}{|\vec{v}|}

siendo

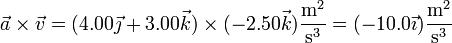
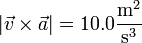
\vec{a}\times\vec{v}=(4.00\vec{\jmath}+3.00\vec{k})\times(-2.50\vec{k})\frac{\mathrm{m}^2}{\mathrm{s}^3} = (-10.0\vec{\imath})\frac{\mathrm{m}^2}{\mathrm{s}^3}        |\vec{v}\times\vec{a}|=10.0\frac{\mathrm{m}^2}{\mathrm{s}^3}

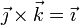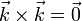(no es necesario hallar el determinante; es más corto multiplicar término a término y aplicar que \vec{\jmath}\times\vec{k}=\vec{\imath} y \vec{k}\times\vec{k}=\vec{0}).

Obtenemos la aceleración normal

a_n = \frac{10.0}{5.00}\frac{\mathrm{m}}{\mathrm{s}^2}=2.00\frac{\mathrm{m}}{\mathrm{s}^2}

La aceleración normal puede también hallarse a partir de los módulos de la aceleración completa y la tangencial

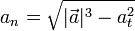
a_n = \sqrt{|\vec{a}|^3-a_t^2}

4 Radio de curvatura

Una vez que tenemos la rapidez y la aceleración normal calculamos el radio de curvatura

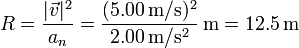
R = \frac{|\vec{v}|^2}{a_n}= \frac{(5.00\,\mathrm{m}/\mathrm{s})^2}{2.00\,\mathrm{m}/\mathrm{s}^2}\,\mathrm{m}=12.5\,\mathrm{m}

5 Posición un tiempo más tarde

Para hallar la posición en un instante posterior no nos basta con los datos de la posición, la velocidad y la aceleración en un instante dado. No sabemos cómo cambian en el tiempo estas cantidades y por tanto no disponemos de información suficiente para responder a esta pregunta.

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculos_a_partir_de_magnitudes_cinem%C3%A1ticas_instant%C3%A1neas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace