Frenado de un fórmula 1
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Cuando el Ferrari de Fernando Alonso se acerca a la ''chicane'' de Monza, su velocidad a 150 m de ésta es de 340 km/h. Cuando entra en la ''chicane'…') |
|||
| Línea 7: | Línea 7: | ||
==Aceleración en el SI== | ==Aceleración en el SI== | ||
| + | Pasamos en primer lugar los valores de la velocidad al SI. A 150m de la chicane tiene una velocidad de | ||
| + | |||
| + | <center><math>x_1 = -150\,\mathrm{m}\qquad\qquad v_1 = 340\frac{\mathrm{km}}{\mathrm{h}}\times \frac{10\,\mathrm{m}/\mathrm{s}}{36\,\mathrm{km}/\mathrm{h}} = 94.4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y al entrar en la chicane | ||
| + | |||
| + | <center><math>x_2 = 0\,\mathrm{m}\qquad\qquad v_2 = 80\frac{\mathrm{km}}{\mathrm{h}}\times \frac{10\,\mathrm{m}/\mathrm{s}}{36\,\mathrm{km}/\mathrm{h}} = 22.2\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Para hallar la aceleración aplicamos que en un movimiento uniformemente acelerado | ||
| + | |||
| + | <center><math>x(t) = x_0 + v_0t + \frac{1}{2}a t^2\qquad\qquad v(t)=v_0+a t</math></center> | ||
| + | |||
| + | En este caso no conocemos lo que tarda en llegar a la chicane, pero no es necesario. tenemos dos ecuaciones y dos incógnitas (la aceleración y el intervalo de frenado). | ||
| + | |||
| + | Si contamos como instante inicial el del comienzo de la frenada, ya tenemos <math>x_0</math> y <math>v_0</math>. Para el final de la frenada nos queda | ||
| + | |||
| + | x_2 = x_1 + v_1 t + \frac{1}{2}at^2 \qquad v_2 = v_1 + a t | ||
| + | |||
==“Fuerzas G”== | ==“Fuerzas G”== | ||
==Velocidad como función de la posición== | ==Velocidad como función de la posición== | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | ||
Revisión de 16:26 16 oct 2012
Contenido |
1 Enunciado
Cuando el Ferrari de Fernando Alonso se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 340 km/h. Cuando entra en la chicane va a 80 km/h.
- Suponiendo que la aceleración es constante, determine su valor.
- Exprese el resultado en el SI y como un múltiplo de g (siendo
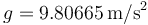 ).
).
- Determine la velocidad como función de la posición y represéntela gráficamente.
2 Aceleración en el SI
Pasamos en primer lugar los valores de la velocidad al SI. A 150m de la chicane tiene una velocidad de
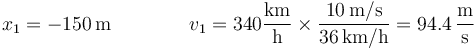
y al entrar en la chicane
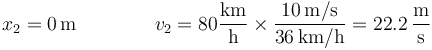
Para hallar la aceleración aplicamos que en un movimiento uniformemente acelerado

En este caso no conocemos lo que tarda en llegar a la chicane, pero no es necesario. tenemos dos ecuaciones y dos incógnitas (la aceleración y el intervalo de frenado).
Si contamos como instante inicial el del comienzo de la frenada, ya tenemos x0 y v0. Para el final de la frenada nos queda
x_2 = x_1 + v_1 t + \frac{1}{2}at^2 \qquad v_2 = v_1 + a t





