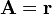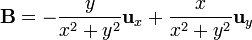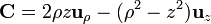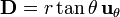Campos vectoriales en diferentes sistemas

(Diferencias entre revisiones)

Revisión de 10:33 25 sep 2008

Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:

$\mathbf{A} = \mathbf{r}\,$
$\mathbf{B} = -\dfrac{y}{x^2+y^2}\mathbf{u}_{x}+\dfrac{x}{x^2+y^2}\mathbf{u}_{y}$
$\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}$
$\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}$

@@ Línea 8: / Línea 8: @@
 ==Solución==
+===Primer campo===
+===Segundo campo===
 [[Categoría:Problemas de fundamentos matemáticos]]