Coordenadas esféricas. Base vectorial
De Laplace
(→Base vectorial) |
(→Factores de escala) |
||
| Línea 24: | Línea 24: | ||
==Factores de escala== | ==Factores de escala== | ||
| + | Para la coordenada <math>\varphi</math>, al tratarse de la misma que en cilíndricas, tendríamos que | ||
| + | |||
| + | <center><math>h_\varphi= \rho</math></center> | ||
| + | |||
| + | pero, ¡alto!, <math>\rho</math> no es una coordenada esférica. Para escribir este resultado correctamente, debemos escribirlo todo en esféricas, así: | ||
| + | |||
| + | <center><math>h_\varphi= r\,\mathrm{sen}\,\theta</math></center> | ||
| + | |||
| + | La coordenada <math>r\,</math> es una distancia, por lo que su factor de escala es | ||
| + | |||
| + | <center><math>h_r=1\,</math></center> | ||
| + | |||
| + | mientras que <math>$\theta$\,</math> es un ángulo, lo que hace que la distancia recorrida sea el radio por el ángulo, y | ||
| + | |||
| + | <center><math>h_\theta = r\,</math></center> | ||
==Artículo siguiente== | ==Artículo siguiente== | ||
Revisión de 20:17 20 nov 2007
Contenido |
1 Base vectorial
La coordenada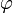 
es la misma que en cilíndricas, por lo que su vector unitario es también el mismo
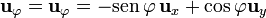
Para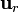 
y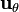 
construimos un nuevo triángulo rectángulo, éste sobre un plano 
.
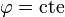El vector 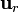va en la dirección radial, por lo que se relaciona con la base cilíndrica como
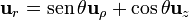
y, sustituyendo la relación con la base cartesiana
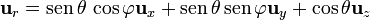
mientras que 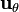es tangente al meridiano de radio 
y apunta hacia el sur
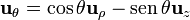
y, en términos de la base cartesiana,
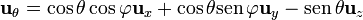
2 Factores de escala
Para la coordenada 
, al tratarse de la misma que en cilíndricas, tendríamos que
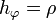
pero, ¡alto!, ρ no es una coordenada esférica. Para escribir este resultado correctamente, debemos escribirlo todo en esféricas, así:
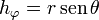
La coordenada es una distancia, por lo que su factor de escala es
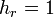
mientras que 
es un ángulo, lo que hace que la distancia recorrida sea el radio por el ángulo, y
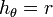
3 Artículo siguiente
El vector de posición y otros ejemplos
4 Artículo anterior
Coordenadas cilíndricas. Base vectorial
