Densidades de carga eléctrica GIA
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Enunciado == Calcula la carga eléctrica total en cada uno de estos sistemas # Uno hilo recto de longitud <math>L</math> con una densidad lineal de carga uniforme <math>\lamb…') |
(→Enunciado) |
||
| Línea 7: | Línea 7: | ||
# Una esfera de radio <math>R</math> con densidad de carga volumétrica uniforme <math>\rho_0</math>. | # Una esfera de radio <math>R</math> con densidad de carga volumétrica uniforme <math>\rho_0</math>. | ||
# Una esfera de radio <math>R</math> con densidad de carga volumétrica <math>\rho(r)=A\,r</math>, siendo <math>r</math> la distancia al centro de la esfera. | # Una esfera de radio <math>R</math> con densidad de carga volumétrica <math>\rho(r)=A\,r</math>, siendo <math>r</math> la distancia al centro de la esfera. | ||
| + | |||
| + | [[Categoría:Problemas de campo eléctrico F2 GIA]] | ||
== Solución == | == Solución == | ||
última version al 01:52 10 mar 2012
1 Enunciado
Calcula la carga eléctrica total en cada uno de estos sistemas
- Uno hilo recto de longitud L con una densidad lineal de carga uniforme λ0.
- Un hilo recto de longitud L con densidad lineal de carga
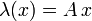 (x = 0 corresponde al punto medio).
(x = 0 corresponde al punto medio).
- Un hilo circular con densidad de carga lineal uniforme λ0.
- Un disco de radio R y grosor nulo con densidad superficial de carga uniforme σ0.
- Una esfera de radio R con densidad de carga volumétrica uniforme ρ0.
- Una esfera de radio R con densidad de carga volumétrica
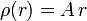 , siendo r la distancia al centro de la esfera.
, siendo r la distancia al centro de la esfera.
2 Solución
2.1 Esfera de radio R con 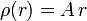
Consideramos que la esfera está formada por cortezas esféricas concéntricas cada una de radio r y grosor dr, con 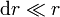 . Debido a esta condición, puede despreciarse la curvatura de cada una de estas cortezas esféricas, y su volumen es el de un paralelepípedo de base el área de la corteza y altura dr
. Debido a esta condición, puede despreciarse la curvatura de cada una de estas cortezas esféricas, y su volumen es el de un paralelepípedo de base el área de la corteza y altura dr
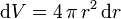
El dr es tan pequeño que en el volumen de cada corteza esférica la densidad de carga puede considerarse constante. Así pues, la carga de cada corteza es
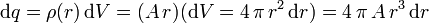
La carga total de la esfera es la suma de la carga de todas las cortezas que podemos considerar variando su radio desde 0 hasta R. Es decir