Campo eléctrico de un plano cargado GIA
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 12: | Línea 12: | ||
<center><math>\sigma_e (\mathbf{r}')=\sigma_0\simeq\frac{Q}{S}\,\mathrm{,}\,</math></center> | <center><math>\sigma_e (\mathbf{r}')=\sigma_0\simeq\frac{Q}{S}\,\mathrm{,}\,</math></center> | ||
| - | siendo <math>S</math> el área de la superficie cargada. En conscuencia, la validez de este modelo y de los resultados que de él se deriven, se restringirá a la región del espacio que comprende puntos alejados de los bordes de la superficie | + | siendo <math>S</math> el área de la superficie cargada. En conscuencia, la validez de este modelo y de los resultados que de él se deriven, se restringirá a la región del espacio que comprende puntos suficientemente alejados de los bordes de la superficie cargada, a la vez que tan próximos a ella como para que su tamaño pueda considerarse infinito. |
| + | |||
===Campo eléctrico de un plano=== | ===Campo eléctrico de un plano=== | ||
Revisión de 11:29 9 mar 2012
1 Enunciado
- Calcúlese el campo eléctrico a ambos lados del plano.
- Se dispone ahora otro plano, paralelo al anterior a una distancia d, y con una densidad superficial de carga uniforme − σ0. Halle el campo eléctrico en todos los puntos del espacio.
2 Solución
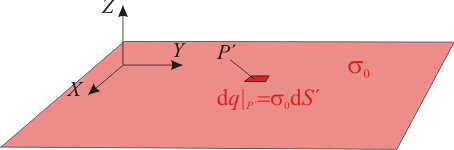
El plano infinito Π con una densidad superficial de carga eléctrica constante σ0, es un modelo en primera aproximación del sistema consistente en una región plana de área de espesor despreciable donde hay distribuida una cantidad de carga Q. Además, la región es lo suficientemente extensa como para poder considerar que, en puntos P' que se hallan lejos de la bordes, la carga se distribuye de manera uniforme, según la función densidad superficial de carga,
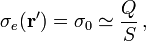
siendo S el área de la superficie cargada. En conscuencia, la validez de este modelo y de los resultados que de él se deriven, se restringirá a la región del espacio que comprende puntos suficientemente alejados de los bordes de la superficie cargada, a la vez que tan próximos a ella como para que su tamaño pueda considerarse infinito.
