Curva de potencial quebrada
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula de masa <math>m=1\,\mathrm{kg}</math> se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la…') |
|||
| Línea 9: | Línea 9: | ||
==Primer punto de retorno== | ==Primer punto de retorno== | ||
| + | La partícula se encuentra inicialmente en <math>x = 2\,\mathrm{m}</math>. De acuerdo con la gráfica, la energía potencial en este punto vale | ||
| + | |||
| + | <center><math>U(x=2\,\mathrm{m})=-1\,\mathrm{J}</math></center> | ||
| + | |||
| + | Además de esta energía potencial, la partícula posee una cierta energía cinética, de valor | ||
| + | |||
| + | <center><math>K = \frac{1}{2}mv_0^2 = \frac{1}{2}\left(1\,\mathrm{kg}\right)\left(2\,\frac{\mathrm{m}}{\mathrm{s}}\right)^2 = 2\,\mathrm{J}</math></center> | ||
| + | |||
| + | con lo que la energía mecánica de la partícula vale en el instante inicial | ||
| + | |||
| + | <center><math>E = K + U = 2\,\mathrm{J}-1\,\mathrm{J}=+1\,\mathrm{J}</math></center> | ||
| + | |||
| + | Puesto que la partícula se encuentra sometida solo a una fuerza conservativa, esta energía permanece constante, lo que se representa en la gráfica por una línea horiozntal | ||
| + | |||
| + | <center>[[Archivo:curva-potencial-quebrada-02.png]]</center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
==Movimiento entre puntos de retorno== | ==Movimiento entre puntos de retorno== | ||
==Disipación de energía== | ==Disipación de energía== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 20:46 21 ene 2012
Contenido |
1 Enunciado
Una partícula de masa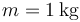 
se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. Inicialmente se encuentra en 
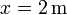moviéndose hacia el semieje OX negativo con velocidad 
.
- ¿En qué punto se detiene por primera vez?
- ¿Qué tipo de movimiento describe la partícula entre
y un punto de retorno?
- Suponga que la masa se ve sometida adicionalmente a una fuerza de rozamiento que la va frenando hasta detenerla por completo. ¿Cuánta energía se disipa hasta que se detiene?
2 Primer punto de retorno
La partícula se encuentra inicialmente en 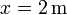. De acuerdo con la gráfica, la energía potencial en este punto vale
Además de esta energía potencial, la partícula posee una cierta energía cinética, de valor
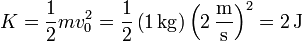
con lo que la energía mecánica de la partícula vale en el instante inicial
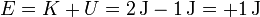
Puesto que la partícula se encuentra sometida solo a una fuerza conservativa, esta energía permanece constante, lo que se representa en la gráfica por una línea horiozntal
