Balanza de frutero
De Laplace
(Página creada con '== Enunciado == Una balanza de frutero cuelga verticalmente de forma que cuándo sólo está el plato, de masa 200 g, la elongación respecto de la elongación natural es de 1.…')
Edición más nueva →
Revisión de 13:45 10 ene 2012
Contenido |
1 Enunciado
Una balanza de frutero cuelga verticalmente de forma que cuándo sólo está el plato, de masa 200 g, la elongación respecto de la elongación natural es de 1.00 cm. De pronto, el frutero suelta 1.00 kg de plátanos en el plato. Despreciando el rozamiento,
- ¿Cuál es la amplitud de las oscilaciones resultantes?
- Cuál es su período?
- ¿Cuál es la velocidad máxima de los plátanos?
- ¿Cuánto vale la energía mecánica del sistema si tomamos como referencia de alturas la posición inicial del plato?
- Supón que, estando en el punto más bajo de sus oscilaciones, uno de los plátanos (de 100 g de masa) cae del plato. ¿Cuál es la amplitud de las oscilaciones que hace el plato a partir de ese momento?
2 Solución
2.1 Constante del resorte
Cuando sólo está colgando el plato vacío (masa 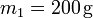 ), las fuerzas sobre éste son su peso y la fuerza del resorte. Siguiendo la figura, escogemos el eje X apuntando hacia abajo, de modo que el origen está en el punto de anclaje del muelle. Cuando no está el plato, el extremo del muelle está en x0 (la elongación natural). Al colgar el plato, la posición de equilibrio se obtiene cuando la fuerza del muelle equilibra el peso del plato
), las fuerzas sobre éste son su peso y la fuerza del resorte. Siguiendo la figura, escogemos el eje X apuntando hacia abajo, de modo que el origen está en el punto de anclaje del muelle. Cuando no está el plato, el extremo del muelle está en x0 (la elongación natural). Al colgar el plato, la posición de equilibrio se obtiene cuando la fuerza del muelle equilibra el peso del plato
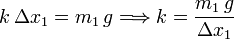
La elongación respecto a la elongación natural es
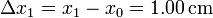
por lo que la constante del muelle es
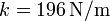
2.2 Amplitud de las oscilaciones
Las oscilaciones del muelle vienen dadas por la expresión
s(t) = Acos(ωt + φ)
donde s(t) es la posición del plato respecto de la posición de equilibrio. Las constantes A y φ se determinan a partir de las condiciones iniciales.
Al añadir los plátanos, de masa 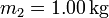 , la posición de equilibrio cambia. En esa nueva posición de equilibrio el resorte debe compensar el peso de del plato y los plátanos. La elongación de equilibrio respecto a la elongación natural se obtiene de
, la posición de equilibrio cambia. En esa nueva posición de equilibrio el resorte debe compensar el peso de del plato y los plátanos. La elongación de equilibrio respecto a la elongación natural se obtiene de
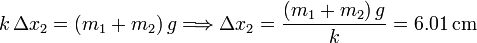
donde Δx2 = x2 − x0.
Justo al añadir los plátanos, el plato está más alto que la nueva posición de equilibrio. Así pues, el valor inicial de s(t) es
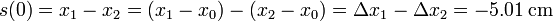
La velocidad inicial es cero, pues parte del reposo.
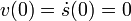
Ahora podemos determinar las constantes A y φ
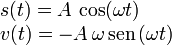
2.3 Período
La frecuencia angular depende del valor de la constante del resorte y de la masa que oscila
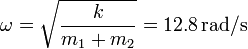
El período de oscilación es
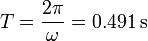
2.4 Velocidad máxima
La velocidad en cada instante es
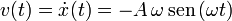
El valor máximo de la velocidad es