Sistemas simples de sólidos rígidos
De Laplace
(→Movimiento de un sólido libre) |
|||
| Línea 19: | Línea 19: | ||
==Movimiento de un sólido libre== | ==Movimiento de un sólido libre== | ||
Cuando sobre un sólido la resultante de las fuerzas y el momento resultante se anulan | Cuando sobre un sólido la resultante de las fuerzas y el momento resultante se anulan | ||
| + | |||
| + | <center><math>\vec{F}=\vec{0}\qquad\qquad\vec{M}_O=\vec{0}</math></center> | ||
| + | |||
| + | ello no implica que el sólido esté necesariamente en reposo, solo que no se ve acelerado. El estado de reposo es solo un caso particular. | ||
| + | |||
| + | En general, lo que podemos afirmar es que la cantidad de movimiento y el momento cinético permanecen constantes | ||
| + | |||
| + | <center><math>\vec{p}=\mathrm{cte}\qquad\qquad \vec{L}_O=\mathrm{cte}</math></center> | ||
| + | |||
| + | Estas dos ecuaciones implican que también se conserva el momento cinético respecto al centro de masas | ||
| + | |||
| + | <center><math>\vec{L}'=\mathrm{cte}</math></center> | ||
| + | |||
| + | y puesto que la potencia desarrollada sobre el sólido es nula también se conserva su energía cinética | ||
| + | |||
| + | <center><math>K = \frac{1}{2}M|\vec{v}_C|^2 + \frac{1}{2}\vec{\omega}\cdot\vec{L}'</math></center> | ||
| + | |||
| + | De la conservación de la cantidad de movimiento se deduce que el centro de masas se mueve con un movimiento rectilíneo y uniforme. | ||
| + | |||
| + | <center><math>\vec{v}_C=\mathrm{cte}</math></center> | ||
| + | |||
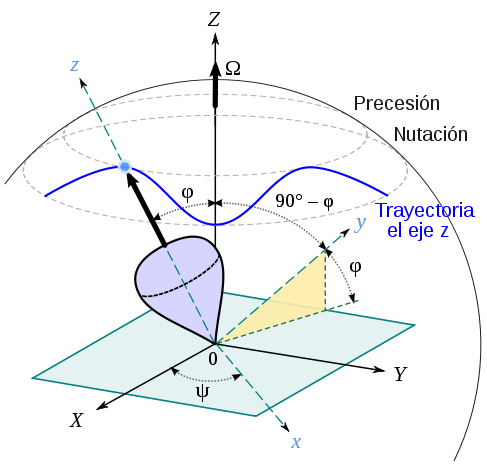
| + | La analogía entre traslación y rotación nos sugiere que la conservación del momento cinético implica que la velocidad angular es constante, pero esto no es cierto en general. Lo más que podemos afirmar en general es que la componente de la velocidad angular en la dirección del momento cinético sí permanece constante. Pero las componentes en otras direcciones pueden variar. El sólido puede desarrollar un movimiento de ''precesión'' en el cual el sólido gira en torno a un eje instantáneo de rotación, que está rotando a su vez. | ||
| + | |||
| + | En el caso de un sólido simétrico, como una esfera o un cubo, en el que la velocidad angular es paralela al momento cinético, la conservación del segundo implica la constancia de la primera | ||
| + | |||
| + | <center><math>\vec{L}_O = I\vec{\omega}\qquad \vec{L}_O=\mathrm{cte}\qquad\Rightarrow\qquad \vec{\omega}=\mathrm{cte}</math></center> | ||
| + | |||
| + | Incluso en el caso de que la velocidad del CM y la velocidad angular permanezcan constantes, el movimiento de los partículas de un sólido libre puede ser muy complicado. Así, por ejemplo, en el caso de un sólido formado por [[Dos_partículas_unidas_por_una_barra_(GIE)|dos partículas unidas por una barra]], el movimiento de cada una puede ser una cicloide | ||
| + | |||
| + | <center>[[Archivo:barrarotante.gif]]</center> | ||
| + | |||
| + | |||
| + | |||
==Giróscopo== | ==Giróscopo== | ||
Revisión de 22:24 3 ene 2012
Contenido |
1 Introducción
Las aplicaciones de la dinámica del sólido rígido son incalculables ya que gran parte de la teoría de máquinas y mecanismos puede realizarse suponiendo que los distintos componentes son aproximadamente rígidos. La mayoría de estas aplicaciones, incluso las de apariencia sencilla, no obstante, suele implicar complejos cálculos matemáticos, por lo que escapan al alcance de esta introducción.
2 Estática del sólido
La estática del sólido (y de los sistemas de sólidos) es el estudio de las condiciones en que un sólido o sistema permanece en reposo. Matemáticamente la expresión de la condición de equilibrio es muy simple:

Sin embargo, la aplicación práctica de estas ecuaciones es mucho más complicada, ya que a menudo una o varias de las fuerzas que actúan sobre el sólido son fuerzas de reacción vincular, cuyo valor es desconocido a priori y que son incógnitas adicionales del problema. Normalmente, un problema de estática de sólidos se compone de varios elementos:
- Determinación de la(s) posición(es) de equilibrio posibles, si existen.
- Cálculo de las fuerzas y pares de reacción vincular.
Adicionalmente, suele existir una parte que requiere el estudio de la energía del sistema y del comportamiento de éste cuando se somete a una perturbación:
- Determinación de la estabilidad de los puntos de equilibrio.
Como ejemplo sencillo, tenemos el estudio del equilibrio de una barra apoyada en el suelo y en una pared.
3 Movimiento de un sólido libre
Cuando sobre un sólido la resultante de las fuerzas y el momento resultante se anulan

ello no implica que el sólido esté necesariamente en reposo, solo que no se ve acelerado. El estado de reposo es solo un caso particular.
En general, lo que podemos afirmar es que la cantidad de movimiento y el momento cinético permanecen constantes

Estas dos ecuaciones implican que también se conserva el momento cinético respecto al centro de masas
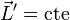
y puesto que la potencia desarrollada sobre el sólido es nula también se conserva su energía cinética

De la conservación de la cantidad de movimiento se deduce que el centro de masas se mueve con un movimiento rectilíneo y uniforme.
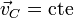
La analogía entre traslación y rotación nos sugiere que la conservación del momento cinético implica que la velocidad angular es constante, pero esto no es cierto en general. Lo más que podemos afirmar en general es que la componente de la velocidad angular en la dirección del momento cinético sí permanece constante. Pero las componentes en otras direcciones pueden variar. El sólido puede desarrollar un movimiento de precesión en el cual el sólido gira en torno a un eje instantáneo de rotación, que está rotando a su vez.
En el caso de un sólido simétrico, como una esfera o un cubo, en el que la velocidad angular es paralela al momento cinético, la conservación del segundo implica la constancia de la primera

Incluso en el caso de que la velocidad del CM y la velocidad angular permanezcan constantes, el movimiento de los partículas de un sólido libre puede ser muy complicado. Así, por ejemplo, en el caso de un sólido formado por dos partículas unidas por una barra, el movimiento de cada una puede ser una cicloide

4 Giróscopo
5 Ley de la palanca
6 Vuelco inminente
7 Movimiento de una peonza pesada