Propiedades dinámicas de un sólido rígido
De Laplace
(→Momento cinético) |
|||
| Línea 93: | Línea 93: | ||
nos queda | nos queda | ||
| - | <center><math>\vec{L}' = m_1\vec{r}^{\,,}_1\times(\vec{\omega}\times\vec{r}_1^{\,,})+m_1\vec{r}^{\,,}_2\times(\vec{\omega}\times\vec{r} | + | <center><math>\vec{L}' = m_1\vec{r}^{\,,}_1\times(\vec{\omega}\times\vec{r}_1^{\,,})+m_1\vec{r}^{\,,}_2\times(\vec{\omega}\times\vec{r}_2^{\,,})</math></center> |
Debido al doble producto vectorial, esta expresión es bastante más compleja que la de la cantidad de movimiento, por lo que solo consideraremos los casos más sencillos. | Debido al doble producto vectorial, esta expresión es bastante más compleja que la de la cantidad de movimiento, por lo que solo consideraremos los casos más sencillos. | ||
| + | |||
| + | Supongamos una partícula <math>m_1</math> que describe una circunferencia de radio <math>R_1</math> en torno al CM con velocidad angular <math>\vec{\omega}</math>. El momento cinético de esta partícula respecto al centro de la circunferencia es perpendicular al plano de ésta y de módulo | ||
| + | |||
| + | <center><math>|\vec{L}'_1| = m_1|\vec{r}'_1||\vec{v}'_1| = m_1(R_1)(\omega R_1) = m_1R_1^2\omega</math></center> | ||
| + | |||
| + | Puesto que en este caso el momento cinético tiene la misma dirección y sentido que la velocidad angular, podemos escribir esta expresión en forma vectorial | ||
| + | |||
| + | <center><math>\vec{L}'_1 = m_1R_1^2\vec{\omega}</math></center> | ||
| + | |||
| + | Si ahora consideramos un sólido simétrico (como un disco, una esfera o un cilindro) que gira en torno un eje dado que pasa por el CM, cada uno de los puntos ontribuye de manera análoga y el momento cinético total respecto al CM vale | ||
| + | |||
| + | <center><math>\vec{L}'=\left(m_1R_1^2+m_2R_2^2+\cdots\right)\vec{\omega}=I\vec{\omega}</math></center> | ||
| + | |||
| + | siendo <math>R_i</math> la distancia de cada punto al eje e <math>I</math> una nueva magnitud conocida como ''momento de inercia'' (que se discute con más detalle más adelante). | ||
| + | |||
| + | Esta igualdad nos dice que el momento cinético de un sólido simétrico respecto a un eje que pasa por su CM es proporcional a la velocidad angular con la que gira, de manera análoga a cómo la cantidad de movimiento es proporcional a la velocidad del CM. La constante de proporcionalidad es el ''momento de inercia'', que desempeña el papel de la masa en cuanto a medida de la inercia del sólido respecto a una rotación. | ||
| + | |||
| + | La igualdad anterior no siempre es cierta, ya que para una partícula el momento cinético respecto a un punto que no es el centro de la circunferencia que describe (aunque sea del eje de rotación) no será en general paralelo a la velocidad angular. Sólo para sólidos que tienen este eje como de simetría se cancelan las componentes no paralelas y resulta una situación de paralelismo entre <math>\vec{L}'</math> y <math>\vec{\omega}</math>. | ||
==Momento de inercia== | ==Momento de inercia== | ||
Revisión de 22:23 27 dic 2011
Contenido |
1 Introducción
A la hora de establecer las ecuaciones de la dinámica del sólido rígido se debe, en primer lugar, definir qué magnitudes lo caracterizan, para poder escribir correctamente las ecuaciones de evolución.
2 Masa
En cinemática del sólido rígido no es necesario considerar la extensión real del sólido. Puede describirse el campo de velocidades suponiendo que se extiende a todos los puntos del espacio tanto interiores como exteriores al sólido, sin importar si en estos puntos existe una partícula material o no.
En dinámica, en cambio, sí es importante considerar la extensión finita del sólido. Un sólido real ocupa un volumen V que por definición es indeformable (aunque puede trasladarse y rotar en el espacio). En este volumen existe una serie de partículas, con masas mi de forma que el sólido posee una masa total
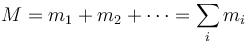
Para la mayoría de los sólidos, no obstante, es preferible modelarlos como un continuo que llena toda una región del espacio. En cada elemento de volumen dV existe una pequeña cantidad de sólido relacionada con el volumen a través de la densidad de masa
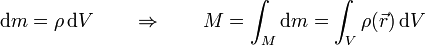
En un sólido homogéneo la densidad de masa es la misma en todos sus puntos y
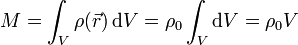
Así para sólidos homogéneos de formas:
- Paralelepípedo:
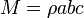
- Cilindro

- Esfera
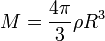
En ocasiones puede suponerse que un sólido se reduce a una fina lámina. Se define entonces la densidad superficial de masa, σ,
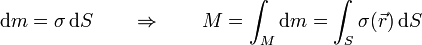
que, para el caso de un sólido homogéneo nos da
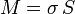
Así, por ejemplo, para una hoja tamaño A4 de 80 g/m² su masa es
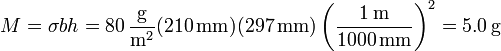
Aplicando las fórmulas del área de una superficie cilíndrica o esférica obtenemos las masas

3 Cantidad de movimiento
La cantidad de movimiento de un sólido es igual a la suma de la cantidad de movimiento de cada una de las partículas que lo componen
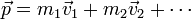
Por tratarse de un sólido, estas velocidades verifican el teorema de Chasles
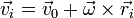
lo cual, al sustituir en la expresión de la cantidad de movimiento nos da
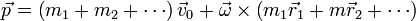
El primero de los dos paréntesis es la masa total del sólido, mientras que el segundo nos da la posición del centro de masas
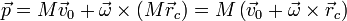
Por otro lado, la cantidad de movimiento de un sistema de partículas se relaciona con la velocidad del centro de masas
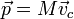
Igualando ambas expresiones obtenemos la velocidad del centro de masas del sólido
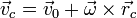
Esta igualdad simplemente nos dice que el centro de masas se mueve rígidamente con el sólido estando siempre en la misma posición relativa a éste (aunque el CM puede no coincidir con ninguna de las partículas del sólido, se mueve como una más de ellas).
4 Momento cinético
El momento cinético del sólido equivale a la suma de los momentos cinéticos de cada una de las partículas que lo componen
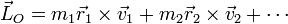
Este momento cinético puede descomponerse en una parte debida al movimiento con el centro de masas más otra debida al movimiento alrededor del centro de masas
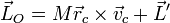
siendo
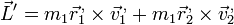
Si aquí sustituimos la expresión del campo de velocidades de un sólido,
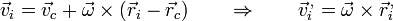
nos queda

Debido al doble producto vectorial, esta expresión es bastante más compleja que la de la cantidad de movimiento, por lo que solo consideraremos los casos más sencillos.
Supongamos una partícula m1 que describe una circunferencia de radio R1 en torno al CM con velocidad angular  . El momento cinético de esta partícula respecto al centro de la circunferencia es perpendicular al plano de ésta y de módulo
. El momento cinético de esta partícula respecto al centro de la circunferencia es perpendicular al plano de ésta y de módulo
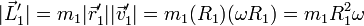
Puesto que en este caso el momento cinético tiene la misma dirección y sentido que la velocidad angular, podemos escribir esta expresión en forma vectorial
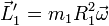
Si ahora consideramos un sólido simétrico (como un disco, una esfera o un cilindro) que gira en torno un eje dado que pasa por el CM, cada uno de los puntos ontribuye de manera análoga y el momento cinético total respecto al CM vale
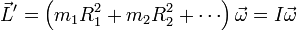
siendo Ri la distancia de cada punto al eje e I una nueva magnitud conocida como momento de inercia (que se discute con más detalle más adelante).
Esta igualdad nos dice que el momento cinético de un sólido simétrico respecto a un eje que pasa por su CM es proporcional a la velocidad angular con la que gira, de manera análoga a cómo la cantidad de movimiento es proporcional a la velocidad del CM. La constante de proporcionalidad es el momento de inercia, que desempeña el papel de la masa en cuanto a medida de la inercia del sólido respecto a una rotación.
La igualdad anterior no siempre es cierta, ya que para una partícula el momento cinético respecto a un punto que no es el centro de la circunferencia que describe (aunque sea del eje de rotación) no será en general paralelo a la velocidad angular. Sólo para sólidos que tienen este eje como de simetría se cancelan las componentes no paralelas y resulta una situación de paralelismo entre 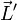 y
y  .
.





