Propiedades dinámicas de un sólido rígido
De Laplace
(→Cantidad de movimiento) |
(→Cantidad de movimiento) |
||
| Línea 58: | Línea 58: | ||
lo cual, al sustituir en la expresión de la cantidad de movimiento nos da | lo cual, al sustituir en la expresión de la cantidad de movimiento nos da | ||
| - | <center><math>\vec{p}=\left(m_1+m_2+\cdots)\vec{v}_0+\vec{\omega}\times\left(m_1\vec{r}_1+m\vec{r}_2+\cdots\right)</math></center> | + | <center><math>\vec{p}=\left(m_1+m_2+\cdots\right)\vec{v}_0+\vec{\omega}\times\left(m_1\vec{r}_1+m\vec{r}_2+\cdots\right)</math></center> |
El primero de los dos paréntesis es la masa total del sólido, mientras que el segundo nos da la posición del centro de masas | El primero de los dos paréntesis es la masa total del sólido, mientras que el segundo nos da la posición del centro de masas | ||
Revisión de 19:35 27 dic 2011
Contenido |
1 Introducción
A la hora de establecer las ecuaciones de la dinámica del sólido rígido se debe, en primer lugar, definir qué magnitudes lo caracterizan, para poder escribir correctamente las ecuaciones de evolución.
2 Masa
En cinemática del sólido rígido no es necesario considerar la extensión real del sólido. Puede describirse el campo de velocidades suponiendo que se extiende a todos los puntos del espacio tanto interiores como exteriores al sólido, sin importar si en estos puntos existe una partícula material o no.
En dinámica, en cambio, sí es importante considerar la extensión finita del sólido. Un sólido real ocupa un volumen V que por definición es indeformable (aunque puede trasladarse y rotar en el espacio). En este volumen existe una serie de partículas, con masas mi de forma que el sólido posee una masa total
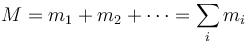
Para la mayoría de los sólidos, no obstante, es preferible modelarlos como un continuo que llena toda una región del espacio. En cada elemento de volumen dV existe una pequeña cantidad de sólido relacionada con el volumen a través de la densidad de masa
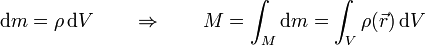
En un sólido homogéneo la densidad de masa es la misma en todos sus puntos y
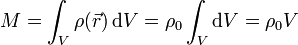
Así para sólidos homogéneos de formas:
- Paralelepípedo:
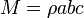
- Cilindro

- Esfera
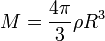
En ocasiones puede suponerse que un sólido se reduce a una fina lámina. Se define entonces la densidad superficial de masa, σ,
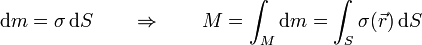
que, para el caso de un sólido homogéneo nos da
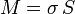
Así, por ejemplo, para una hoja tamaño A4 de 80 g/m² su masa es
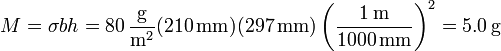
Aplicando las fórmulas del área de una superficie cilíndrica o esférica obtenemos las masas

3 Cantidad de movimiento
La cantidad de movimiento de un sólido es igual a la suma de la cantidad de movimiento de cada una de las partículas que lo componen
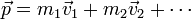
Por tratarse de un sólido, estas velocidades verifican el teorema de Chasles
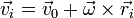
lo cual, al sustituir en la expresión de la cantidad de movimiento nos da
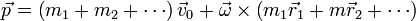
El primero de los dos paréntesis es la masa total del sólido, mientras que el segundo nos da la posición del centro de masas
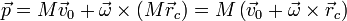
Por otro lado, la cantidad de movimiento de un sistema de partículas se relaciona con la velocidad del centro de masas
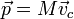
Igualando ambas expresiones obtenemos la velocidad del centro de masas del sólido
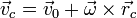
Esta igualdad simplemente nos dice que el centro de masas se mueve rígidamente con el sólido estando siempre en la misma posición relativa a éste (aunque el CM puede no coincidir con ninguna de las partículas del sólido, se mueve como una más de ellas).





