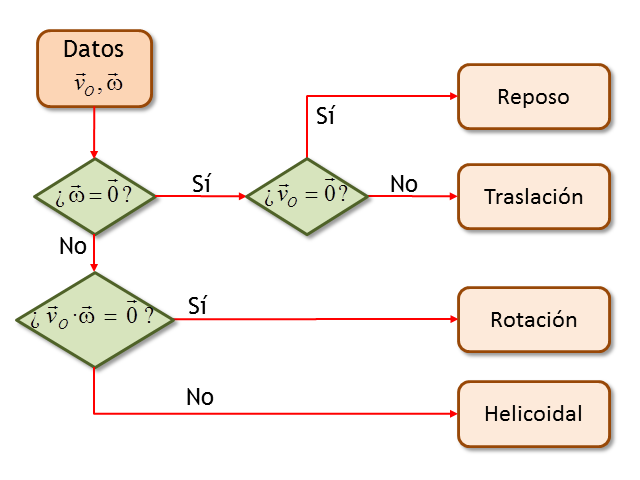
Clasificación de movimientos de un sólido (versión 2011)
De Laplace
(→Ejes instantáneos) |
|||
| Línea 301: | Línea 301: | ||
<center><math>\vec{r}_E=\vec{r}_I+\lambda\vec{\omega}\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}x & = & (-4+2\mu )\,\mathrm{cm} \\ y & = & -4\,\mathrm{cm} \\ z & = & (8+\mu)\,\mathrm{cm}\end{array}\right.</math></center> | <center><math>\vec{r}_E=\vec{r}_I+\lambda\vec{\omega}\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}x & = & (-4+2\mu )\,\mathrm{cm} \\ y & = & -4\,\mathrm{cm} \\ z & = & (8+\mu)\,\mathrm{cm}\end{array}\right.</math></center> | ||
| + | ===Caso V=== | ||
| + | Por último, tenemos de nuevo una rotación con velocidades | ||
| + | |||
| + | <center><math>2\vec{\imath}+2\vec{\jmath}+2\vec{k}\qquad\qquad-0.2\vec{\imath}-0.1\vec{k}</math></center> | ||
==Propiedades del sistema de partículas== | ==Propiedades del sistema de partículas== | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
Revisión de 10:50 17 dic 2011
Contenido |
1 Enunciado
Se tiene un sólido formado por ocho masas iguales, 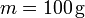 , situadas en los vértices de un cubo de lado
, situadas en los vértices de un cubo de lado 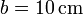 . En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
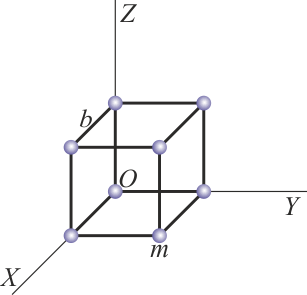
Considere los casos siguientes para las velocidades de las masas situadas en 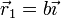 ,
, 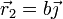 y
y 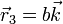
| Caso | 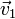 (cm/s) (cm/s)
| 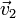 (cm/s) (cm/s)
| 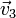 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 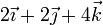
| 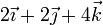
| 
|
| II | 
| 
| 
|
| III | 
| 
| 
|
| IV | 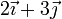
| 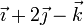
| 
|
| V | 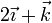
| 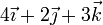
| 
|
| VI | 
| 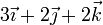
| 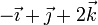
|
- Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
- Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
- Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
- Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.
2 Condición cinemática de rigidez
Para que una distribución de velocidades corresponda a un posible movimiento de un sólido rígido, debe satisfacer la condición cinemática de rigidez, que establece que para cada par de puntos la velocidad relativa debe ser ortogonal a la posición relativa

o empleando las posiciones y velocidades medidas respecto a un sistema fijo
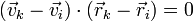
Para cada uno de los seis casos se cumple, midiendo las distancias en centímetros
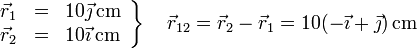
y análogamente

Comprobamos entonces la condición cinemática de rigidez para cada uno de los seis casos.
Así en el caso I se cumple:
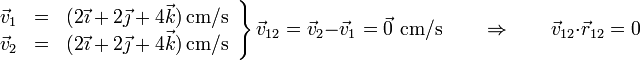
Operando igualmente para el resto de pares y para el resto de casos queda la siguiente tabla:
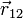 (cm) (cm)
| 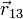 (cm) (cm)
| 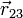 (cm) (cm)
| ||||
|---|---|---|---|---|---|---|
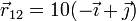
| 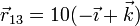
| 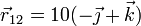
| ||||
| Caso | 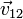 (cm/s) (cm/s)
| 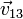 (cm/s) (cm/s)
| 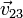 (cm/s) (cm/s)
| 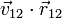 (cm/s) (cm/s)
| 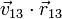 (cm/s) (cm/s)
| 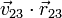 (cm/s) (cm/s)
|
| I | 
| 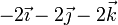
| 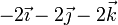
| 
| 
| 
|
| II | 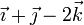
| 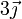
| 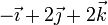
| 
| 
| 
|
| III | 
| 
| 
| 
| 
| 
|
| IV | 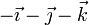
| 
| 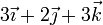
| 
| 
| 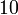
|
| V | 
| 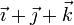
| 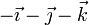
| 
| 
| 
|
| VI | 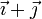
| 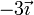
| 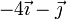
| 
| 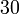
| 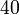
|
Vemos que el caso IV y el caso VI no cumplen la condición cinemática de rigidez y no pueden ser movimientos rígidos.
3 Caso general
En general, dada la velocidad de tres puntos no alineados, es posible determinar la velocidad del origen y la velocidad angular de cualquier sólido. Existen atajos que permiten caracterizar el movimiento como las propiedades siguientes:
- Si tres puntos no alineados tienen la misma velocidad, el movimiento es de traslación.
- Si dos tienen la misma velocidad y el tercero no, el movimiento es de rotación o helicoidal con eje uno paralelo a la recta que pasa por los dos puntos de la misma velocidad.
En este problema, no obstante, es sencillo determinar el campo de velocidades simplemente a partir del sistema de ecuaciones vectoriales
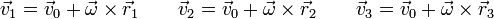
donde 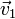 ,
, 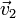 y
y 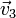 son datos conocidos. Las incógnitas son las componentes de
son datos conocidos. Las incógnitas son las componentes de  y
y 
Así, para la primera tenemos
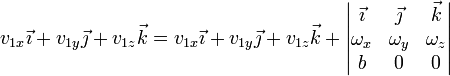
donde 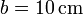 es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema
es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema
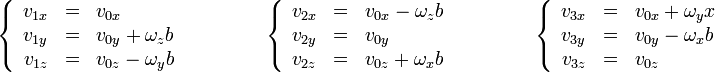
De las ecuaciones primera, cuarta y novena es inmediata la velocidad del origen
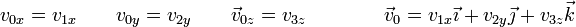
Una vez que tenemos la velocidad del origen, podemos hallar las componentes de la velocidad angular sustituyendo  y despejando
y despejando
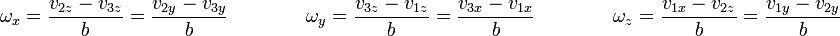
El que haya dos expresiones para cada componente de la velocidad angular se debe a que las velocidades no son completamente independientes, sino que deben satisfacer la condición cinemática de rigidez. Si al hallar, por ejemplo ωx por la primera fracción y por la segunda salieran valores diferentes, querría decir que las velocidades no pueden pertenecer a un sólido rígido (esta es otra forma de comprobar la condición de rigidez).
4 Clasificación de los movimientos
Aplicando esto a los cuatro casos que nos quedan obtenemos las siguientes velocidades para el origen y para la velocidad angular, así como para el producto escalar de estas dos:
| Caso | 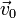 (cm/s) (cm/s)
|  (rad/s) (rad/s)
| 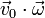 (cm/s²) (cm/s²)
|
|---|---|---|---|
| I | 
| 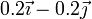
| 
|
| II | 
| 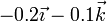
| 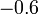
|
| III | 
| 
| 
|
| V | 
| 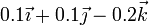
| 0 |
Los casos con velocidad angular distinta de cero, pero ortogonales a la velocidad del origen corresponden a rotaciones fijas. Las que no son ortogonales corresponden a movimientos helicoidales. Esto da la siguiente tabla de resultados
| Caso | Estado |
|---|---|
| I | Rotación |
| II | Helicoidal |
| III | Traslación |
| IV | Imposible |
| V | Rotación |
| VI | Imposible |
5 Ejes instantáneos
Los movimientos I y V son rotaciones y por tanto poseen un eje instantáneo de rotación (EIR); el movimiento II es helicoidal y posee un eje instantáneo de rotación y mínimo deslizamiento (EIRMD). Existen varias formas de hallar las ecuaciones de los ejes:
- Ecuaciones paramétricas
- La ecuación para ambos tipos de ejes es la misma. Se localiza un punto del eje con la fórmula
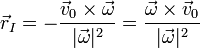
- y la ecuación del eje es la recta que pasa por este punto y lleva la dirección de la velocidad angular
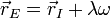
- Ecuaciones implícitas
- En el caso de los movimientos de rotación pura es inmediato obtener las ecuaciones implícitas del EIR, ya que lo forman aquellos puntos que tienen velocidad nula, por lo que basta con hacer
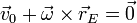
- En el caso de los movimientos helicoidales es un poco más complicado, ya que previamente hay que calcular la velocidad de deslizamiento con la que los puntos del eje avanzan a lo largo de él.
Aplicando esto a los tres casos posibles, nos queda:
5.1 Caso I
En este caso tenemos una rotación pura con velocidad del origen y velocidad angular

y obtenemos el punto del eje
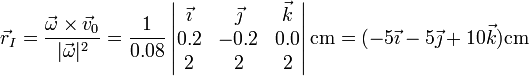
La posición de un punto arbitrario del eje será entonces
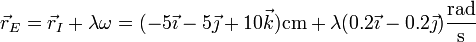
Esto se puede abreviar haciendo μ = 0.2λ y queda
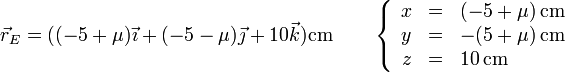
Alternativamente, por tratarse de una rotación pura, el eje se puede escribir en forma vectorial
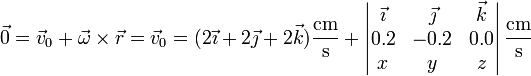
donde las coordenadas se miden en centímetros.
Desarrollando y separando por componentes quedan las ecuaciones implícitas
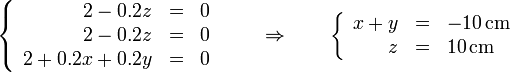
5.2 Caso II
En el segundo caso tenemos un movimiento helicoidal con velocidad del origen y angular

lo que nos da un punto del EIRMD
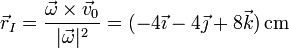
y de aquí quedan las ecuaciones paramétricas del eje

5.3 Caso V
Por último, tenemos de nuevo una rotación con velocidades