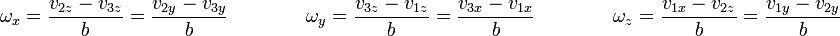Clasificación de movimientos de un sólido (versión 2011)
De Laplace
(→Caso general) |
(→Caso general) |
||
| Línea 159: | Línea 159: | ||
<center><math>\vec{v}_1 = \vec{v}_0+\vec{\omega}\times\vec{r}_1\qquad \vec{v}_2 = \vec{v}_0+\vec{\omega}\times\vec{r}_2\qquad \vec{v}_3 = \vec{v}_0+\vec{\omega}\times\vec{r}_3</math></center> | <center><math>\vec{v}_1 = \vec{v}_0+\vec{\omega}\times\vec{r}_1\qquad \vec{v}_2 = \vec{v}_0+\vec{\omega}\times\vec{r}_2\qquad \vec{v}_3 = \vec{v}_0+\vec{\omega}\times\vec{r}_3</math></center> | ||
| + | |||
| + | donde <math>\vec{v}_1</math>, <math>\vec{v}_2</math> y <math>\vec{v}_3</math> son datos conocidos. Las incógnitas son las componentes de <math>\vec{v}_0</math> y <math>\vec{\omega}</math> | ||
Así, para la primera tenemos | Así, para la primera tenemos | ||
| Línea 166: | Línea 168: | ||
donde <math>b=10\,\mathrm{cm}</math> es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema | donde <math>b=10\,\mathrm{cm}</math> es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema | ||
| - | <center><math>\left\{\begin{array}{rcl}v_{1x}& = & v_{0x} \\ v_{1y} & = & v_{0y}+\omega_z b \\ v_{1z} & = & v_{0z}-\omega_y b \end{array}\right.\qquad\qquad \left\{\begin{array}{ | + | <center><math>\left\{\begin{array}{rcl}v_{1x}& = & v_{0x} \\ v_{1y} & = & v_{0y}+\omega_z b \\ v_{1z} & = & v_{0z}-\omega_y b \end{array}\right.\qquad\qquad \left\{\begin{array}{rcl}v_{2x} & = & v_{0x}-\omega_z b \\ v_{2y}& = & v_{0y} \\ v_{2z} & = & v_{0z}+\omega_x b \end{array}\right.\qquad\qquad \left\{\begin{array}{rcl}v_{3x} & = & v_{0x}+\omega_y x \\ v_{3y}& = & v_{0y}-\omega_x b \\ v_{3z} & = & v_{0z} \end{array}\right.</math></center> |
| + | |||
| + | De las ecuaciones primera, cuarta y novena es inmediata la velocidad del origen | ||
| + | |||
| + | <center><math>v_{0x} = v_{1x}\qquad v_{0y}=v_{2y}\qquad \vec{v}_{0z}=v_{3z}\qquad \qquad \vec{v}_0=v_{1x}\vec{\imath}+v_{2y}\vec{\jmath}+v_{3z}\vec{k}</math></center> | ||
| + | |||
| + | Una vez que tenemos la velocidad del origen, podemos hallar las componentes de la velocidad angular sustituyendo <math>\vec{v}_0</math> y despejando | ||
| + | |||
| + | <center><math>\omega_x = \frac{v_{2z}-v_{3z}}{b}=\frac{v_{2y}-v_{3y}}{b}\qquad \qquad \omega_y = \frac{v_{3z}-v_{1z}}{b}=\frac{v_{3x}-v_{1x}}{b}\qquad \qquad \omega_z = \frac{v_{1x}-v_{2z}}{b}=\frac{v_{1y}-v_{2y}}{b}</math></center> | ||
==Clasificación de los movimientos== | ==Clasificación de los movimientos== | ||
Revisión de 23:40 16 dic 2011
Contenido |
1 Enunciado
Se tiene un sólido formado por ocho masas iguales, 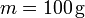 , situadas en los vértices de un cubo de lado
, situadas en los vértices de un cubo de lado 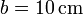 . En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.
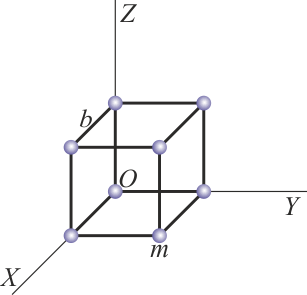
Considere los casos siguientes para las velocidades de las masas situadas en 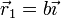 ,
, 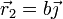 y
y 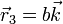
| Caso | 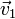 (cm/s) (cm/s)
| 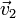 (cm/s) (cm/s)
| 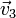 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 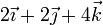
| 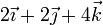
| 
|
| II | 
| 
| 
|
| III | 
| 
| 
|
| IV | 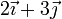
| 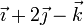
| 
|
| V | 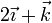
| 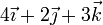
| 
|
| VI | 
| 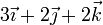
| 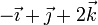
|
- Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
- Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
- Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
- Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.
2 Condición cinemática de rigidez
Para que una distribución de velocidades corresponda a un posible movimiento de un sólido rígido, debe satisfacer la condición cinemática de rigidez, que establece que para cada par de puntos la velocidad relativa debe ser ortogonal a la posición relativa

o empleando las posiciones y velocidades medidas respecto a un sistema fijo
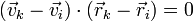
Para cada uno de los seis casos se cumple, midiendo las distancias en centímetros
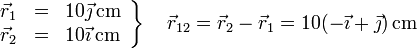
y análogamente

Comprobamos entonces la condición cinemática de rigidez para cada uno de los seis casos.
Así en el caso I se cumple:
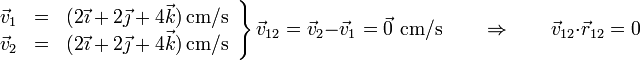
Oprando igualmente para el resto de pares y para el resto de casos queda la siguiente tabla:
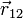 (cm) (cm)
| 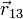 (cm) (cm)
| 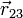 (cm) (cm)
| ||||
|---|---|---|---|---|---|---|
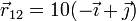
| 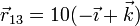
| 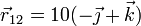
| ||||
| Caso | 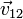 (cm/s) (cm/s)
| 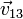 (cm/s) (cm/s)
| 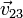 (cm/s) (cm/s)
| 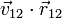 (cm/s) (cm/s)
| 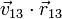 (cm/s) (cm/s)
| 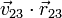 (cm/s) (cm/s)
|
| I | 
| 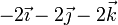
| 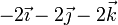
| 
| 
| 
|
| II | 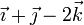
| 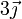
| 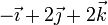
| 
| 
| 
|
| III | 
| 
| 
| 
| 
| 
|
| IV | 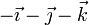
| 
| 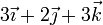
| 
| 
| 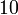
|
| V | 
| 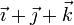
| 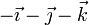
| 
| 
| 
|
| VI | 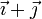
| 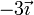
| 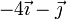
| 
| 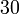
| 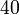
|
Vemos que el caso IV y el caso VI no cumplen la condición cinemática de rigidez y no pueden ser movimientos rígidos.
3 Caso general
En general, dada la velocidad de tres puntos no alineados, es posible determinar la velocidad del origen y la velocidad angular de cualquier sólido. Existen atajos que permiten caracterizar el movimiento como las propiedades siguientes:
- Si tres puntos no alineados tienen la misma velocidad, el movimiento es de traslación.
- Si dos tienen la misma velocidad y el tercero no, el movimiento es de rotación o helicoidal con eje uno paralelo a la recta que pasa por los dos puntos de la misma velocidad.
En este problema, no obstante, es sencillo determinar el campo de velocidades simplemente a partir del sistema de ecuaciones vectoriales
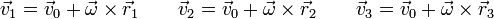
donde 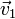 ,
, 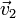 y
y 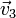 son datos conocidos. Las incógnitas son las componentes de
son datos conocidos. Las incógnitas son las componentes de  y
y 
Así, para la primera tenemos
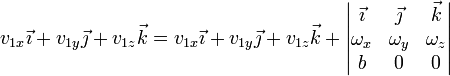
donde 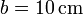 es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema
es la arista del cubo. Desarrollando el producto vectorial y separando por componentes para los tres casos nos queda el sistema
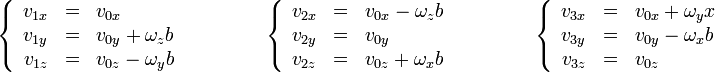
De las ecuaciones primera, cuarta y novena es inmediata la velocidad del origen
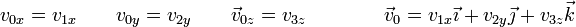
Una vez que tenemos la velocidad del origen, podemos hallar las componentes de la velocidad angular sustituyendo  y despejando
y despejando