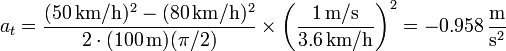Entrar Página Discusión Historial Go to the site toolbox

Cálculo de aceleración en una curva

De Laplace

(Diferencias entre revisiones)
(→Rapidez)
Línea 31: Línea 31:
<center><math>|\vec{v}_1|^2 = |\vec{v}_0|^2 + 2a_t(s_1-s_0)\qquad\Rightarrow\qquad a_t = \frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{2(s_1-s_0)}</math></center>
<center><math>|\vec{v}_1|^2 = |\vec{v}_0|^2 + 2a_t(s_1-s_0)\qquad\Rightarrow\qquad a_t = \frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{2(s_1-s_0)}</math></center>
-
Sustituyendo los datos del enunciado, queda la aceleración tangencial
+
y el cuadrado de la rapidez en cada punto sigue la ecuación lineal
-
<center><math>a_t = \frac{(50\,\mathrm{km}/\mathrm{h})^2-(80\,\mathrm{km}/\mathrm{h})^2}{2\cdot(100\,\mathrm{m})(\pi/2)}\times\left(\frac{1\,\mathrm{m}/\mathrm{s}}{3.6\,\mathrm{km}/\mathrm{h}}\right)^2 = -0.958\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>|\vec{v}|^2 = |\vec{v}_0|^2+\frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{(s_1-s_0)}(s-s_0)</math></center>
A este resultado se puede llegar también despejando de las ecuaciones del movimiento uniformemente acelerado para el movimiento a lo largo de la carretera
A este resultado se puede llegar también despejando de las ecuaciones del movimiento uniformemente acelerado para el movimiento a lo largo de la carretera
Línea 39: Línea 39:
<center><math>s = s_0 + |\vec{v}|_0 t + \frac{1}{2}a_tt^2\qquad |\vec{v}|=|\vec{v}|_0+a_t t</math></center>
<center><math>s = s_0 + |\vec{v}|_0 t + \frac{1}{2}a_tt^2\qquad |\vec{v}|=|\vec{v}|_0+a_t t</math></center>
-
Una vez que tenemos la aceleración tangencial constante podemos hallar la rapidez en cualquier instante,  
+
El resultado se puede poner en función del ángulo girado <math>\varphi</math>, aplicando que <math>s(\varphi)=R\varphi</math>
-
<center><math>|\vec{v}|^2 = |\vec{v}_0|^2+2a_t s\qquad\Rightarrow\qquad |\vec{v}|=\sqrt{|\vec{v}_0|^2+2a_t s} = \sqrt{|\vec{v}_0|^2+\frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{(s_1-s_0)}(s-s_0)}</math></center>
+
<center><math>|\vec{v}|^2 = |\vec{v}_0|^2+2\varphi \frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{\pi}</math></center>
-
la cual la podemos poner en función del ángulo girado <math>\varphi</math>, aplicando que <math>s(\varphi)=R\varphi</math>
+
Sustituyendo los valores del enunciado queda
-
<center><math> |\vec{v}|= \sqrt{|\vec{v}_0|^2+2\varphi\frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{\pi}}</math></center>
+
<center><math>|\vec{v}|^2 = \left(6400 + 2\varphi\frac{2500-6400}{\pi}\right)\frac{\mathrm{km}^2}{\mathrm{h}^2}= \left(6400 -\frac{7800}{\pi}\varphi\right)\frac{\mathrm{km}^2}{\mathrm{h}^2}</math></center>
 +
 
 +
y una vez que tenemos el cuadrado hallamos la rapidez en cada punto mediante la raíz cuadrada
 +
 
 +
<center><math>|\vec{v}|=\sqrt{6400 -\frac{7800}{\pi}\varphi}\frac{\mathrm{km}}{\mathrm{h}}</math></center>
Aplicando esta fórmula a los valores indicados nos queda la tabla
Aplicando esta fórmula a los valores indicados nos queda la tabla
Línea 77: Línea 81:
==Componentes intrínsecas de la aceleración==
==Componentes intrínsecas de la aceleración==
 +
===Aceleración tangencial===
 +
Sustituyendo los datos del enunciado, queda la aceleración tangencial
 +
 +
<center><math>a_t = \frac{(50\,\mathrm{km}/\mathrm{h})^2-(80\,\mathrm{km}/\mathrm{h})^2}{2\cdot(100\,\mathrm{m})(\pi/2)}\times\left(\frac{1\,\mathrm{m}/\mathrm{s}}{3.6\,\mathrm{km}/\mathrm{h}}\right)^2 = -0.958\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
==Vector aceleración==
==Vector aceleración==
[[Categoría:Problemas de cinemática de la partícula (GIE)]]
[[Categoría:Problemas de cinemática de la partícula (GIE)]]
[[Categoría:Problemas de cinemática tridimensional (GIE)]]
[[Categoría:Problemas de cinemática tridimensional (GIE)]]

Revisión de 08:36 19 oct 2011

Contenido

1 Enunciado

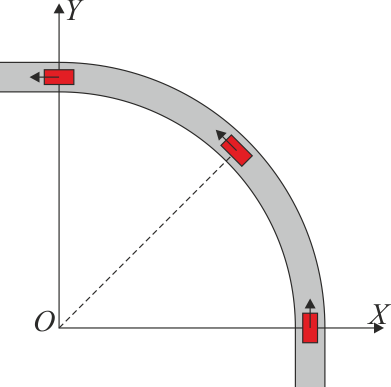
Un coche entra en una curva de 90° y 100 m de radio a 80 km/h. Disminuye su rapidez uniformemente hasta salir de la curva a 50 km/h.

  1. Determine su rapidez cuando ha recorrido 1/3 de la curva, la mitad y 2/3 de ella.
  2. Halle su aceleración tangencial y su aceleración normal en los mismos puntos.
  3. Exprese el vector aceleración en estos puntos en los ejes indicados en la figura
Archivo:aceleracion-coche-curva.png

2 Rapidez

Como en el problema de la aceleración en una recta podría parecer que la rapidez varía linealmente con la posición y por tanto, a mitad de la curva la velocidad se habrá reducido en un 50% de la variación total. Sin embargo, no es así. Lo que es constante en este problema es la derivada respecto al tiempo, no la derivada respecto a la posición.

Se nos dice que

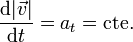
\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=a_t=\mathrm{cte.}

aunque no se nos dice cuánto vale esta cantidad, solo la velocidad en dos puntos conocidos (80 km/h a la entrada y 50 km/h a la salida). Por ello, necesitamos hallar la derivada respecto a la posición. Aplicando la regla de la cadena tenemos

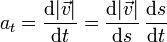
a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t} = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}s}\,\frac{\mathrm{d}s}{\mathrm{d}t}

siendo s la distancia medida a lo largo de la curva. Su derivada respecto al tiempo es la propia rapidez, por lo que

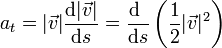
a_t = |\vec{v}|\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}s}= \frac{\mathrm{d}\ }{\mathrm{d}s}\left(\frac{1}{2}|\vec{v}|^2\right)

Por tanto, lo que varía linealmente respecto a la posición no es la rapidez, sino su cuadrado. Podemos integrar aquí y escribir

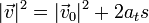
|\vec{v}|^2 = |\vec{v}_0|^2+2a_t s

El valor de at lo obtenemos de que conocemos la rapidez en dos puntos, s0 = 0 (comienzo de la curva) y s1 = πR / 2 (final de la curva), por lo que

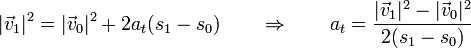
|\vec{v}_1|^2 = |\vec{v}_0|^2 + 2a_t(s_1-s_0)\qquad\Rightarrow\qquad a_t = \frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{2(s_1-s_0)}

y el cuadrado de la rapidez en cada punto sigue la ecuación lineal

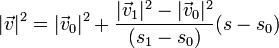
|\vec{v}|^2 = |\vec{v}_0|^2+\frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{(s_1-s_0)}(s-s_0)

A este resultado se puede llegar también despejando de las ecuaciones del movimiento uniformemente acelerado para el movimiento a lo largo de la carretera

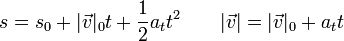
s = s_0 + |\vec{v}|_0 t + \frac{1}{2}a_tt^2\qquad |\vec{v}|=|\vec{v}|_0+a_t t

El resultado se puede poner en función del ángulo girado \varphi, aplicando que 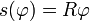s(\varphi)=R\varphi

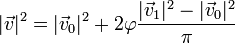
|\vec{v}|^2 = |\vec{v}_0|^2+2\varphi \frac{|\vec{v}_1|^2-|\vec{v}_0|^2}{\pi}

Sustituyendo los valores del enunciado queda

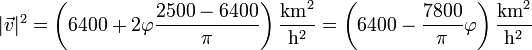
|\vec{v}|^2 = \left(6400 + 2\varphi\frac{2500-6400}{\pi}\right)\frac{\mathrm{km}^2}{\mathrm{h}^2}= \left(6400 -\frac{7800}{\pi}\varphi\right)\frac{\mathrm{km}^2}{\mathrm{h}^2}

y una vez que tenemos el cuadrado hallamos la rapidez en cada punto mediante la raíz cuadrada

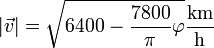
|\vec{v}|=\sqrt{6400 -\frac{7800}{\pi}\varphi}\frac{\mathrm{km}}{\mathrm{h}}

Aplicando esta fórmula a los valores indicados nos queda la tabla

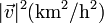
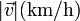
\varphi |\vec{v}|^2 (\mathrm{km}^2/\mathrm{h}^2) |\vec{v}| (\mathrm{km}/\mathrm{h})
0 6400 80.0
π/6 5100 71.4
π/4 4450 66.7
π/6 3800 61.6
π/6 2500 50.0

3 Componentes intrínsecas de la aceleración

3.1 Aceleración tangencial

Sustituyendo los datos del enunciado, queda la aceleración tangencial

a_t = \frac{(50\,\mathrm{km}/\mathrm{h})^2-(80\,\mathrm{km}/\mathrm{h})^2}{2\cdot(100\,\mathrm{m})(\pi/2)}\times\left(\frac{1\,\mathrm{m}/\mathrm{s}}{3.6\,\mathrm{km}/\mathrm{h}}\right)^2 = -0.958\,\frac{\mathrm{m}}{\mathrm{s}^2}

4 Vector aceleración

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_aceleraci%C3%B3n_en_una_curva"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace