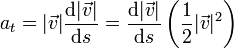Cálculo de aceleración en una curva
De Laplace
| Línea 9: | Línea 9: | ||
==Rapidez== | ==Rapidez== | ||
| + | Como en el problema de la [[Aceleración_en_un_tramo_rectilíneo_(GIE)|aceleración en una recta]] podría parecer que la rapidez varía linealmente con la posición y por tanto, a mitad de la curva la velocidad se habrá reducido en un 50% de la variación total. Sin embargo, no es así. Lo que es constante en este problema es la derivada respecto al tiempo, no la derivada respecto a la posición. | ||
| + | |||
| + | Se nos dice que | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=a_t=\mathrm{cte.}</math></center> | ||
| + | |||
| + | aunque no se nos dice cuánto vale esta cantidad, solo la velocidad en dos puntos conocidos (80 km/h a la entrada y 50 km/h a la salida). Por ello, necesitamos hallar la derivada respecto a la posición. Aplicando la regla de la cadena tenemos | ||
| + | |||
| + | <center><math>a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t} = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}s}\,\frac{\mathrm{d}s}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | siendo <math>s</math> la distancia medida a lo largo de la curva. Su derivada respecto al tiempo es la propia rapidez, por lo que | ||
| + | |||
| + | <center><math>a_t = |\vec{v}|\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}s}= \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}s}\left(\frac{1}{2}|\vec{v}|^2\right)</math></center> | ||
| + | |||
| + | |||
| + | |||
==Componentes intrínsecas de la aceleración== | ==Componentes intrínsecas de la aceleración== | ||
==Vector aceleración== | ==Vector aceleración== | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
[[Categoría:Problemas de cinemática tridimensional (GIE)]] | [[Categoría:Problemas de cinemática tridimensional (GIE)]] | ||
Revisión de 09:01 19 oct 2011
Contenido |
1 Enunciado
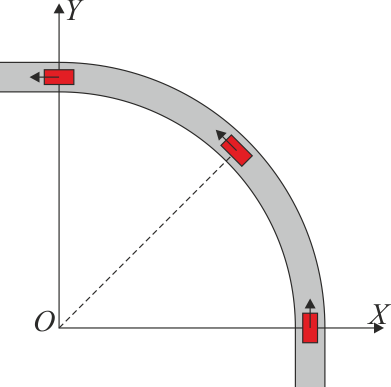
Un coche entra en una curva de 90° y 100 m de radio a 80 km/h. Disminuye su rapidez uniformemente hasta salir de la curva a 50 km/h.
- Determine su rapidez cuando ha recorrido 1/3 de la curva, la mitad y 2/3 de ella.
- Halle su aceleración tangencial y su aceleración normal en los mismos puntos.
- Exprese el vector aceleración en estos puntos en los ejes indicados en la figura
2 Rapidez
Como en el problema de la aceleración en una recta podría parecer que la rapidez varía linealmente con la posición y por tanto, a mitad de la curva la velocidad se habrá reducido en un 50% de la variación total. Sin embargo, no es así. Lo que es constante en este problema es la derivada respecto al tiempo, no la derivada respecto a la posición.
Se nos dice que
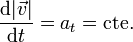
aunque no se nos dice cuánto vale esta cantidad, solo la velocidad en dos puntos conocidos (80 km/h a la entrada y 50 km/h a la salida). Por ello, necesitamos hallar la derivada respecto a la posición. Aplicando la regla de la cadena tenemos
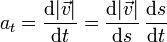
siendo s la distancia medida a lo largo de la curva. Su derivada respecto al tiempo es la propia rapidez, por lo que