Problemas de electrostática en el vacío
De Laplace
(Diferencias entre revisiones)
(Nueva página: ===Una esfera conductora rellena de una densidad de carga=== Una superficie esférica conductora de radio $R$, puesta a tierra, contiene en su interior una distribución de carga ...) |
|||
| Línea 1: | Línea 1: | ||
===[[Una esfera conductora rellena de una densidad de carga]]=== | ===[[Una esfera conductora rellena de una densidad de carga]]=== | ||
| - | Una superficie esférica conductora de radio $R$, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma | + | [[Imagen:esferarhor.gif|right]]Una superficie esférica conductora de radio $R$, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma |
<center><math>\rho =\begin{cases}A r(R-r) & (r< R) \\ 0 & (r>R)\end{cases}</math></center> | <center><math>\rho =\begin{cases}A r(R-r) & (r< R) \\ 0 & (r>R)\end{cases}</math></center> | ||
Revisión de 15:55 7 jul 2008
Una esfera conductora rellena de una densidad de carga
Una superficie esférica conductora de radio $R$, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma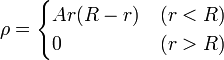
- Calcule el campo eléctrico en todos los puntos del espacio.
- Calcule el valor de la carga almacenada en la esfera conductora.
- Halle el potencial eléctrico en el centro de la esfera.
- A partir del campo eléctrico.
- Por integración directa a partir de las densidades de carga.
- Halle la energía electrostática almacenada en el sistema.






