Entrar Página Discusión Historial Go to the site toolbox

Análisis de problemas de dinámica (GIE)

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Tipos de problemas en dinámica== La segunda ley de Newton relaciona la segunda derivada de la posición con la fuerza que actúa sobre la partícula, la cuál es a su vez una…')
Edición más nueva →

Revisión de 19:00 14 sep 2011

Contenido

1 Tipos de problemas en dinámica

La segunda ley de Newton relaciona la segunda derivada de la posición con la fuerza que actúa sobre la partícula, la cuál es a su vez una función de la posición, la velocidad y el tiempo;

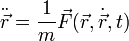
\ddot{\vec{r}}=\frac{1}{m}\vec{F}(\vec{r},\dot{\vec{r}},t)

La solución de esta ecuación constituye el problema fundamental de la dinámica.

Dependiendo de cuáles sean nuestros datos y nuestras incógnitas, podemos tener diferentes clases de problemas:

  • Si conocemos la expresión de la fuerza, junto con las condiciones iniciales del problema (posición y velocidad iniciales de la partícula), podemos emplearla para determinar la posición de la partícula en t > 0. Es lo que se conoce como la dinámica de una partícula no vinculada. Como ejemplos típicos tenemos la caída libre, el oscilador armónico o el movimiento planetario.
  • Si la posición de la partícula está restringida por alguna limitación geométrica o cinemática (por ejemplo, obligada a moverse sobre una superficie), entonces el problema consiste en la determinación del movimiento compatible con esas ligaduras, más la determinación de las fuerzas que producen dichas ligaduras (fuerzas de reacción vincular). Esta es la dinámica de la partícula vinculada.
  • Si conocemos completamente el estado de movimiento de la partícula, podemos emplear la segunda ley de Newton para determinar la fuerza que actúa sobre la partícula. Este es el principio de los dinamómetros, tanto estáticos (con la partícula en equilibrio), como dinámicos (partícula en movimiento).
  • Como caso particular podemos buscar en qué condiciones la partícula permanece en equilibrio y qué fuerzas actúan sobre ella en ese caso. Este es el objeto de la estática.

2 Vínculos o ligaduras

A menudo una partícula no posee libertad de movimiento en el espacio, sino que se encuentra sometida a vínculos (o ligaduras). Un vínculo es una restricción sobre la posición, la velocidad, o una combinación de ambas.

Por ejemplo, una partícula situada sobre una mesa de una altura h puede moverse horizontalmente de manera libre, y podrá moverse verticalmente hacia arriba, pero no hacia abajo ya que la mesa se lo impide.

Matemáticamente escribiríamos esta condición geométrica como

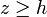
z \geq h

Consideremos ahora un péndulo formado por una barra rígida de longitud l0. La masa situada en su extremo se ve obligada a permanecer a una distancia l0 del punto de anclaje, lo que expresaríamos como

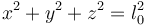
x^2 + y^2 + z^2 = l_0^2

Si en vez de una barra fuera un hilo entonces la condición sería que se encuentra como máximo a una distancia l0

x^2 + y^2 + z^2 \geq l_0^2

Una partícula que se mueve sobre la superficie interior de un cuenco esférico de radio l0 verifica exactamente la misma condición: su distancia al centro es como mucho l0

x^2 + y^2 + z^2 \geq l_0^2

Esto quiere decir que, desde el punto de vista cinemático, es exactamente lo mismo un péndulo flexible que un cuenco esférico. El mecanismo físico en cambio, es diferente.

Las ligaduras también se aplican a las velocidades. Para la partícula en el extremo de un péndulo rígido, la velocidad es siempre perpendicular a la propia barra, lo que se expresa mediante la condición

\vec{v}\cdot\vec{r}=0

Vemos entonces que las ligaduras o vínculos se expresan mediante una ecuación o una inecuación. En el primer caso se denominan ligaduras bilaterales (ya que impiden un movimiento en los dos sentidos); en el segundo son unilaterales (ya que impiden el movimiento en un sentido, pero no en el opuesto).

El efecto de un vínculo es la reducción del número de posibilidades de movimiento, lo que se denominan grados de libertad de la partícula, según la ecuación

r = 3 - h\,

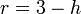
siendo r el número de grados de libertad y h el número de ecuaciones de ligadura. Para el caso del péndulo, tendremos r = 2. Si además está obligado a moverse sobre un plano vertical, h = 2 y r = 1.

2.1 Fuerzas de reacción vincular

Desde el punto de vista cinemático o geométrico es claro lo que representa una ligadura. Ahora bien, ¿cuál es su mecanismo físico?

Imaginemos una mas que cuelga de un péndulo rígido y que se suelta desde el reposo desde una cierta altura. Como consecuencia de la ligadura, la lenteja del péndulo describe un arco de circunferencia. El movimiento que sigue la partícula es acelerado. ¿Qué fuerzas causan la aceleración? Una es claramente el peso, pero si ésta fuera la única, el movimiento de la partícula sería vertical, no circular. Por tanto, debe haber alguna fuera más de manera que se cumpla la segunda ley de Newton, sobre la partícula está actuando una fuerza

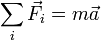
\sum_i \vec{F}_i=m\vec{a}

¿Quién ejerce esta fuerza adicional al peso? No el agente que le comunicó el impulso inicial, ya que ese sólo actuó durante el breve periodo de contacto. La única respuesta posible es que la fuerza la ejerce la propia barra del péndulo. Esta fuerza se denomina en este caso tensión de la barra o más en general fuerza de reacción vincular. Su valor es desconocido a priori (se determina una vez conocida la aceleración).

Microscópicamente las fuerzas de reacción vincular suelen ser fuerzas electromagnéticas. La masa, por acción del peso, tiende a acelerarse verticalmente, pero al hacerlo tira de los átomos de la barra. Por la tercera ley de Newton, éstos tiran de la masa, desviándola de su trayectoria rectilínea.

Las ligaduras son siempre una aproximación (a menudo muy buena) de una situación real, no ideal. Consideremos una masa que cuelga de una barra metálica vertical en reposo. Todo metal posee una cierta elasticidad y, por tanto, al colgarle una masa se estirará ligeramente. Esto provoca la aparición de una fuerza recuperadora de acuierdo con la ley de Hooke

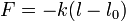
F = -k(l-l_0)\,

En el equilibrio se cumple

k(l-l_0) = mg\qquad\Rightarrow\qquad l = l_0+ \frac{mg}{k}

Cuando suponemos que la rigidez de la barra es muy grande, k tiende a infinito y la deformación es despreciable, quedando l\simeq l_0.

Desde el punto de vista matemático, las fuerzas de reacción vincular suponen incógnitas adicionales para el problema dinámico, pero al haber tantas como ecuaciones de ligadura adicionales, el numero de ecuaciones sigue siendo igual al número de incógnitas.

Hay que destacar que el valor de la fuerza de reacción vincular en una situación dinámica no coincide con el valor de la fuerza de reacción en una situación estática, esto es, depende del estado de movimiento de la partícula.

Generalizando, tenemos el

Principio de liberación
Todo punto material o sistema de puntos materiales sometido a vínculos puede ser tratado como si estuviese libre de los mismos si se sustituyen dichos vínculos por las fuerzas de reacción vincular 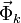\vec{\Phi}_k, las cuales presentan las siguientes características:
  • Cumplen la misma función que los vínculos sustituidos, es decir, se oponen a cualquier estado de reposo o movimiento que sea incompatible con ellos. En el caso de vínculos unilaterales, esto implica que dichas fuerzas solo pueden ir en un sentido. Por ejemplo, la reacción de la mesa siempre irá hacia arriba, pero nunca hacia abajo. Si en la solución de un problema resulta una fuerza de reacción con el sentido incorrecto, el problema debe rehacerse considerando que la ligadura no está presente.
  • Son perpendiculares a los vínculos geométricos cuando éstos consisten en superficies o curvas lisas (sin rozamiento). Por ejemplo, en el caso del péndulo, la lenteja del péndulo se ve obligada a moverse en el interior de una superficie esférica de radio l0, la fuerza de reacción es la tensión de la barra, que apunta necesariamente a largo de sí misma. Esta dirección radial es perpendicular a la superficie esférica de movimiento.

Por tanto, el tratamiento de la dinámica de un punto material vinculado requiere, en virtud del principio de liberación, la incorporación a las ecuaciones de las fuerzas de reacción vincular 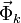\vec{\Phi}_k, las cuales, por ser desconocidas a priori, introducen nuevas incógnitas en el problema matemático.

\begin{cases}\displaystyle\ddot{\vec{r}}=\frac{1}{m}\left[\sum_{i=1}^n\vec{F}_i(t,\vec{r},\dot{\vec{r}}\,)+ \sum_{k=1}^m\vec{\Phi}_k\right] & \\ & \\ \displaystyle f_j(\vec{r},\dot{\vec{r}},t)=0\;\;\;\;\; (\mbox{con}\; j=1,...,h)\;\longrightarrow\; \mbox{ecuaciones de ligadura} & \end{cases}

En esta expresión 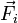\vec{F}_i son las llamadas fuerzas activas, que son aquellas que no son de ligadura, y que se suponen conocidas. En el caso de una partícula no vinculada, todas las fuerzas son activas.

En el ejemplo del péndulo tendríamos las ecuaciones de movimiento, en cartesianas

m\ddot{x} = T_x\qquad m\ddot{y}=T_y\qquad m\ddot{z}=T_z - mg

Tenemos aquí tres ecuaciones y seis incógnitas. Necesitamos tres ecuaciones más. Una es la ecuación de la ligadura

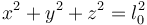
x^2 + y^2 + z^2 = l_0^2\,

Las otras dos las da la condición de que la tensión va en la dirección de la barra, lo que implica paralelismo con el vector de posición

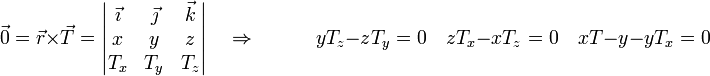
\vec{0}=\vec{r}\times\vec{T}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ x & y & z \\ T_x & T_y & T_z\end{matrix}\right|\quad\Rightarrow\quad \qquad yT_z - zT_y = 0\quad zT_x-xT_z=0\quad xT-y-yT_x = 0

Ahora parece que tenemos más ecuaciones de la cuenta, pero cualquiera de estas tres puede deducirse de las otras dos, así que solo hay dos ecuaciones adicionales.

Por último, señalaremos la importancia de asignar la dirección correcta a las fuerzas de reacción vincular en la medida en que dicha dirección esté predeterminada (por ejemplo, teniendo presente la ortogonalidad de dichas fuerzas a los vínculos geométricos lisos). En buena parte en esto radica el "saber desvincular" una partícula, ya que no podemos olvidar que la compatibilidad del sistema de ecuaciones exige que el número de incógnitas introducidas a través de las fuerzas de reacción vincular sea igual (y no superior) al número h de ecuaciones de ligadura.

3 Diagramas de cuerpo libre

El primer paso para resolver un problema de dinámica vectorial consiste en realizar un diagrama de cuerpo libre. Este es un equema donde aparecen todas las fuerzas aplicadas sobre el cuerpo, incluyendo las fuerzas de reacción que sustituyen a los vínculos.

Así, para el caso del avión tenemos cuatro fuerzas aplicadas

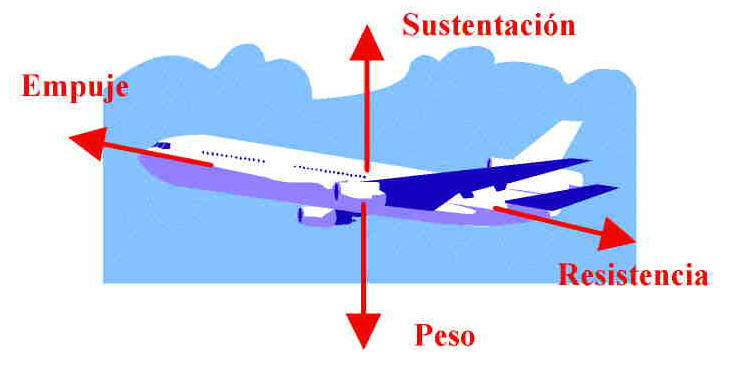
Archivo:fuerzas-avion.jpg

Si un avión asciende con rapidez constante, ¿quiere eso decir que la sustentación es superior al peso? No, porque si asciende uniformemente su aceleración vale cero, y por tanto la resultante de las fuerzas aplicadas es nula. la sustentación y el peso serán iguales. Solo si asciende aceleradamente será la sustentación superior al peso.

Para el péndulo tenemos dos fuerzas actuando sobre la lenteja, siendo una de ellas, la tensión, una fuerza de reacción que sustituye a una ligadura.

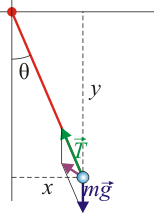
Archivo:fuerzas-pendulo.png

Cuando el péndulo pasa por el punto más bajo, ¿es la tensión de la barra igual al peso? No. La lenteja en ese momento está describiendo un movimiento circular y por tanto posee una aceleración normal además de la tangencial (que se anula en el punto más bajo). La aceleración es radial y hacia adentro, que en este caso es vertical y hacia arriba. Por tanto la tensión será mayor que el peso.

Las dificultades de los diagramas de cuerpo libre suelen aparecer a la hora de dividir el sistema en partes y al considerar las fuerzas de rozamiento.

Consideremos el problema de un caballo que tira de un carro Es evidente que este sistema puede acelerarse en su movimiento. ¿Quién ejerce la fuerza que hace avanzar el sistema?

Supongamos en primer lugar el sistema completo (caballo + carro). Si el caballo va a velocidad constante, ¿hacia adonde apunta la fuerza neta sobre el sistema? ¿Hacia adelante? ¿Hacia atrás? Hacia ningún lado, pues si va a velocidad constante, la fuerza aplicada es nula.

Pero si consideramos por separado las fuerzas externas aplicadas, tenemos que sobre el carro actúa la fuerza de rozamiento sobre el suelo, que va hacia atrás. ¿Dónde está la fuerza externa hacia adelante que la compensa? Decimos, “la produce el caballo” pero eso no puede ser. El caballo es parte del sistema. De acuerdo con la tercera ley de Newton, el carro tira del caballo exactamente con la misma intensidad con la que el animal tira del carro. Por tanto estas dos fuerzas internas se cancelan mutuamente. La fuerza externa que compensa el rozamiento del carro es también una fuerza de rozamiento, la del caballo contra el suelo. El animal empuja con sus pezuñas el suelo hacia atrás. Por tanto, el suelo empuja al caballo hacia adelante. Puesto que la fricción del caballo es superior a la del carro, esta fuerza puede igualar o superar al rozamiento del carro, produciendo movimiento hacia adelante.

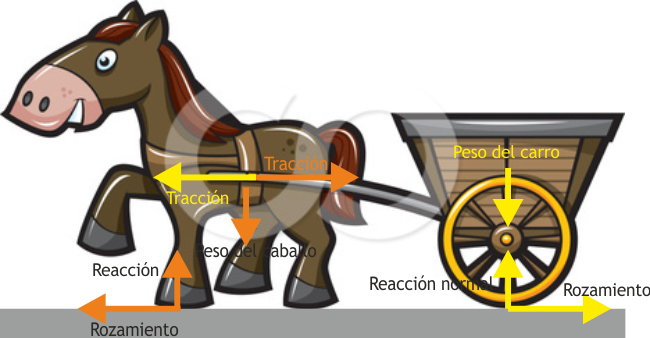
Archivo:caballo-carro.png

Si consideramos solamente el carro entonces tenemos cuatro fuerzas (que, de nuevo, se anulan mutuamente si va a velocidad constante): el peso, la reacción normal del suelo, la fuerza con la que tira el caballo (que ahora es una fuerza externa) y el rozamiento de las rueda.

Si consideramos el caballo de forma aislada, las fuerzas aplicadas sobre él son su peso, la reacción normal del suelo, la fuerza con la que el carro tira del caballo y la que el suelo ejerce sobre el caballo.

4 Determinación del movimiento

4.1 Problema general

4.2 Solución numérica. Método de Euler

En la resolución de las ecuaciones de movimiento,

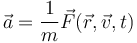
\vec{a}=\frac{1}{m}\vec{F}(\vec{r},\vec{v},t)

incluso en los casos de fuerzas perfectamente conocidas, su integración no es un problema trivial. Al tratarse de una ecuación diferencial, en la que la cantidad a integrar depende de las magnitudes que deseamos hallar, la solución no se limita a una integración respecto al tiempo.

En la mayoría de los problemas no existe solución analítica de las ecuaciones de movimiento. Un ejemplo famoso es el del problema de los tres cuerpos. El movimiento de un cuerpo como un satélite en el campo gravitatorio de otros dos, como la Tierra y la Luna, no puede resolverse analíticamente.

Ello no quiere decir que no pueda hallarse la solución de las ecuaciones de movimiento. Existen diferentes técnicas aproximadas que permiten hallar la solución con la precisión que se desee aunque usualmente requieren el uso de ordenadores. Entre estos métodos aproximados destacan los métodos numéricos, que proporcionan una lista de valores de las variables para una serie de instantes de tiempo.

Dentro de los métodos numéricos para resolver ecuaciones de movimiento, el más sencillo y fácil de interpretar es el método de Euler.

Las ecuaciones de movimiento pueden escribirse como dos ecuaciones para las primeras derivadas

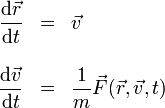
\begin{array}{rcl} \displaystyle \frac{\mathrm{d}\vec{r}}{\mathrm{d}t} & = & \vec{v}\\ && \\ \displaystyle \frac{\mathrm{d}\vec{v}}{\mathrm{d}t} & = & \displaystyle\frac{1}{m}\vec{F}(\vec{r},\vec{v},t) \end{array}

Hacemos entonces la aproximación siguiente: una derivada no es más que un cociente entre dos incrementos infinitamente pequeños. Aproximamos entonces las derivadas por incrementos finitos

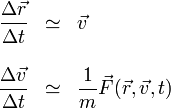
\begin{array}{rcl} \displaystyle \frac{\Delta\vec{r}}{\Delta t} & \simeq & \vec{v}\\ && \\ \displaystyle \frac{\Delta\vec{v}}{\Delta t} & \simeq & \displaystyle\frac{1}{m}\vec{F}(\vec{r},\vec{v},t) \end{array}

Teniendo en cuenta que

\Delta\vec{r}=\vec{r}(t+\Delta t)-\vec{r}(t)\qquad \Delta\vec{v}=\vec{v}(t+\Delta t)-\vec{v}(t)

podemos despejar

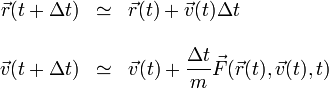
\begin{array}{rcl} \displaystyle \vec{r}(t+\Delta t) & \simeq & \vec{r}(t) + \vec{v}(t)\Delta t\\ && \\ \displaystyle \vec{v}(t+\Delta t) & \simeq & \displaystyle\vec{v}(t) + \frac{\Delta t}{m}\vec{F}(\vec{r}(t),\vec{v}(t),t) \end{array}

lo que nos dice esta aproximación es que si conocemos la posición y la velocidad en un instante dado, podemos aproximar la posición y la velocidad en un instante posterior suponiendo que la velocidad y la fuerza casi no cambian durante el intervalo. La aproximación será mejor cuanto más pequeño sea este intervalo.

Si etiquetamos las sucesivas posiciones y velocidades por un subíndice, nos queda la sucesión

\begin{array}{rcl} t_{n+1} & = & t_n + h \\ && \\ \displaystyle \vec{r}_{n+1} & = & \vec{r}_n + \vec{v}_n h\\ && \\ \displaystyle \vec{v}_{n+1} & = & \displaystyle \vec{v}_n + \frac{h}{m}\vec{F}_n \end{array}

Como ilustración consideremos el caso de un oscilador armónico en una dimensión, que tiene por ecuaciones de movimiento

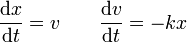
\frac{\mathrm{d}x}{\mathrm{d}t}=v\qquad \frac{\mathrm{d}v}{\mathrm{d}t}=-kx

Este sistema tiene solución analítica, por lo que puede verse cómo de buena es una aproximación.

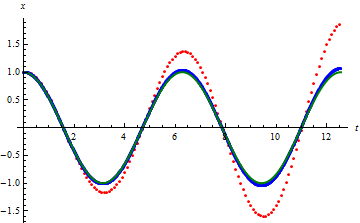
Archivo:oscilador-numerico.png

Para un Δt grande (puntos rojos) resultan oscilaciones, pero que se separan rápidamente de la solución exacta (línea verde). Reduciendo el intervalo de tiempo (puntos azules) se obtiene una mejor aproximación. El coste de esta precisión es que requiere más cálculos y por tanto mayor tiempo de computación. Es necesario entonces hallar un balance entre la precisión deseada y los recursos disponibles.

El método de Euler es muy poco preciso y por ello no se usa en la práctica. Existen métodos mucho más refinados, como el Runge-Kutta, que con los mismos cálculos produce una mucha mejor aproximación al resultado.

4.3 Solución analítica

5 Fuerzas de rozamiento

6 El oscilador armónico

7 Dinámica de la partícula no vinculada

Cuando lo que se conoce son las fuerzas que actúan sobre la partícula así como su posición y velocidad iniciales, la pregunta es ¿cómo se mueve la partícula?

Nuestro punto de partida es la llamada ecuación de movimiento:

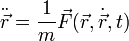
\ddot{\vec{r}}=\frac{1}{m}\vec{F}(\vec{r},\dot{\vec{r}},t)

junto con las condiciones iniciales

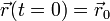
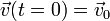
\vec{r}(t=0) = \vec{r}_0        \vec{v}(t=0)=\vec{v}_0

La incógnita de este problema es la ecuación horaria 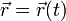\vec{r}=\vec{r}(t), o equivalentemente, las tres funciones x(t), y(t), z(t) (o variables equivalentes). El que debamos determinar tres coordenadas nos dice que el número de grados de libertad del problema es 3.

r = 3\,

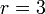
En el caso de que conozcamos la fuerza como función del tiempo solamente, la respuesta es sencilla: basta con integrar dos veces respecto al tiempo

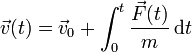
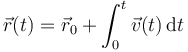
\vec{v}(t) = \vec{v}_0 + \int_0^t\frac{\vec{F}(t)}{m}\,\mathrm{d}t        \vec{r}(t) = \vec{r}_0+\int_0^t\vec{v}(t)\,\mathrm{d}t

Lo normal, sin embargo, es que la fuerza no se conozca como función del tiempo, sino como función de la posición (como en el caso de la ley de la Gravitación Universal), de la velocidad (por ejemplo, la fuerza de Lorentz sobre una carga en movimiento es proporcional a la velocidad) y en ocasiones del tiempo. Esto quiere decir que para poder determinar la posición como función del tiempo, debemos integrar una función... que no conocemos hasta que hayamos determinado la propia posición. Esta aparente circularidad convierte a esta fórmula en lo que se conoce como una ecuación diferencial y hace que su integración no sea en absoluto trivial. De hecho, en solo algunos casos es posible determinar analíticamente la posición incluso aunque se conozca perfectamente la fuerza.

En numerosas situaciones de interés, es preciso recurrir a la integración numérica, en la cual se obtiene la posición, con una cierta precisión, con ayuda de ordenadores. Por ejemplo, el movimiento de la Tierra respecto al Sol puede determinarse exactamente, si solo consideramos estos dos astros, pero el movimiento del sistema Tierra-Luna alrededor del Sol es imposible de resolver analíticamente y requiere de técnicas aproximadas.

La segunda ley de Newton puede descomponerse en un sistema de ecuaciones para las coordenadas cartesianas de la partícula

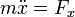
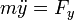
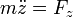
m\ddot{x} = F_x        m\ddot{y}=F_y        m\ddot{z}=F_z

siendo Fx, Fy y Fz las componentes cartesianas de la fuerza

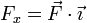
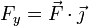
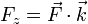
F_x = \vec{F}\cdot\vec{\imath}        F_y = \vec{F}\cdot\vec{\jmath}        F_z = \vec{F}\cdot\vec{k}

Estas ecuaciones no son independientes porque cada componente de la fuerza dependerá en general de las tres coordenadas.

Como ilustración de un problema importante de dinámica de partícula no vinculada tenemos el caso de la caída libre de un cuerpo, con y sin rozamiento con el aire.

8 Problemas

Curvas y peraltes

Obtenido de "http://tesla.us.es/wiki/index.php/An%C3%A1lisis_de_problemas_de_din%C3%A1mica_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace