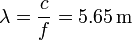Onda sonora en agua
De Laplace
(Página creada con '== Enunciado == Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50…') |
(→Solución) |
||
| Línea 7: | Línea 7: | ||
== Solución == | == Solución == | ||
| - | + | [[Imagen:Onda_sonora_en_agua.png|600px|right]] | |
Si ''H'' es la profundidad del lecho marino, la distancia entre el barco y el pecio es | Si ''H'' es la profundidad del lecho marino, la distancia entre el barco y el pecio es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | d = \dfrac{H}{\ | + | d = \dfrac{H}{\mathrm{sen}\,\alpha} = 100\,\mathrm{m} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 17: | Línea 17: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | c = \dfrac{2\,d}{\Delta t} = \dfrac{2\ | + | c = \dfrac{2\,d}{\Delta t} = \dfrac{2\times100\,\mathrm{m}}{0.135\,\mathrm{s}} = 1.48\,\mathrm{km/s} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 30: | Línea 30: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | B = \rho\,c^2 = | + | B = \rho\,c^2 = 2.32\times10^9\,\mathrm{Pa} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 42: | Línea 42: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | |\Delta P| = B\dfrac{\Delta V}{V} = | + | |\Delta P| = B\dfrac{\Delta V}{V} = 2.32\times10^9\,\mathrm{Pa} \times 0.01 = |
| - | + | 2.32\times10^7\,\mathrm{Pa} = 229\,\mathrm{atm} | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 51: | Línea 51: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lambda = \dfrac{c}{f} = | + | \lambda = \dfrac{c}{f} = 5.65\,\mathrm{m} |
</math> | </math> | ||
</center> | </center> | ||
Revisión de 14:24 12 ene 2011
1 Enunciado
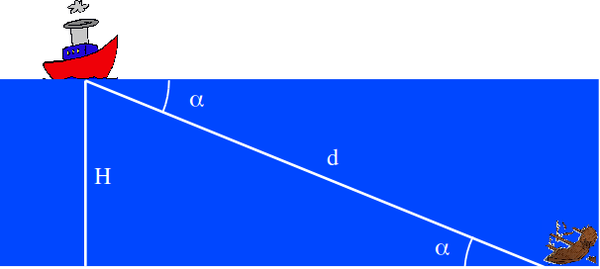
Un barco usa un sistema de sonar para detectar objetos submarinos. El barco se encuentra en reposo en una zona en la que la profundidad del lecho marino es de 50.0 metros. El sistema emite un haz de ondas de sonido de frecuencia f = 262 Hz que forma un ángulo de 30.0º con la superficie del mar y mide el tiempo que tarda la onda, que se refleja en un pecio, en regresar al detector. Sabiendo que el tiempo de retardo es 0.135 segundos y que la densidad del agua es 1.06×10³ kg/m³, calcule
- La velocidad del sonido en el agua
- El módulo de compresibilidad del agua
- La longitud de onda de la señal emitida.
2 Solución
Si H es la profundidad del lecho marino, la distancia entre el barco y el pecio es
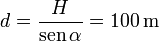
El intervalo de tiempo que nos dan es el tiempo que la onda tarda en ir y volver desde el barco hasta el pecio. Por tanto la velocidad de la onda sonora en el agua es
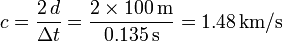
La velocidad del sonido en el agua es
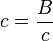
donde B es el módulo de compresibilidad y ρ es la densidad volumétrica del agua. Entonces
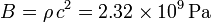
El módulo de compresibilidad mide la resistencia de un medio a cambiar su volumen cuando es comprimido. Por definición
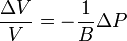
Un medio con un valor grande de B varía muy poco su volumen cuando es sometido a un incremento de presión ΔP. Con el dato obtenido para B, para variar en un 1% el volumen de una masa de agua, la sobrepresión necesaria es
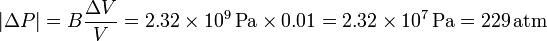
Es decir, el agua es esencialmente incompresible.
La longitud de onda de la onda sonora es