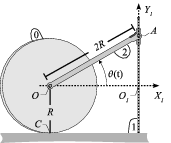Disco articulado con una varilla (G.I.A.)

De Laplace

(Diferencias entre revisiones)

Pedro (Discusión | contribuciones)
(Página creada con '== Enunciado == right El mecanismo de la figura está formado por un disco (sólido "0"), de radio <math>R</math>; y por una varilla …')
Edición más nueva →

Revisión de 16:50 27 dic 2010

1 Enunciado

El mecanismo de la figura está formado por un disco (sólido "0"), de radio $R$ ; y por una varilla $O A$ (sólido "2"), de longitud $2 R$ , articulada en su extremo $O$ al centro del disco. El disco rueda sin deslizar sobre la recta fija (sólido "1") de ecuación $y 1 = - R$ , mientras que el extremo $A$ de la varilla está obligado a deslizar sobre el eje $O 1 Y 1$ . Sabiendo que el mecanismo se mueve conforme a la ley horaria $θ(t) = ω t$ (donde $ω$ es una constante conocida), se pide:

Los vectores de posición, 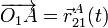$\overrightarrow{O_1A}=\vec{r}_{21}^A(t)$ ; velocidad, 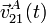$\vec{v}_{21}^A(t)$ ; y aceleración 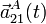$\vec{a}_{21}^A(t)$ , del movimiento absoluto del extremo $A$ de la varilla. ¿Qué tipo de movimiento describe dicho punto?
Reducciones cinemáticas (vectores velocidad angular y velocidad de un punto) de los movimientos {21}, {01} y {20}.
Determinación gráfica y analítica de la posición del C.I.R. del movimiento {21}.

2 Solución

2.1 Cálculo del vector de posición, velocidad y aceleración del punto A en el movimiento {21}

El extremo $A$ de la varilla está situado siempre sobre el eje $O 1 Y 1$ . Su posición puede determinarse en la escuadra "1" como

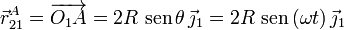
$\vec{r}_{21}^A=\overrightarrow{O_1A} = 2R\,\,\mathrm{sen}\,\theta\,\vec{\jmath}_1=2R\,\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}_1$

Como esta expresión es válida en todo instante y está expresada en la base del sólido "1", podemos derivarla para calcular la velocidad y la aceleración pedidas

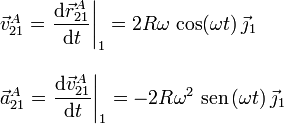
$\begin{array}{l} \vec{v}_{21}^A = \left.\dfrac{\mathrm{d}\vec{r}_{21}^A}{\mathrm{d}t}\right|_1=2R\omega\,\cos(\omega t)\,\vec{\jmath}_1\\ \\ \vec{a}_{21}^A = \left.\dfrac{\mathrm{d}\vec{v}_{21}^A}{\mathrm{d}t}\right|_1=-2R\omega^2\,\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}_1 \end{array}$

Para determinar el tipo de movimiento que realiza el punto $A$ , observemos que se cumple

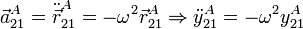
$\vec{a}_{21}^A=\ddot{\vec{r}}_{21}^A=-\omega^2\vec{r}_{21}^A\Rightarrow \ddot{y}_{21}^A=-\omega^2{y}_{21}^A$

Es decir, es un movimiento armónico simple a lo largo del eje $O 1 Y 1$ , centrado en $O 1$ , de frecuencia $ω$ y amplitud $2 R$ .

2.2 Reducciones cinemáticas de los movimientos

2.2.1 Movimiento {21}

Hemos calculado 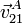$\vec{v}_{21}^A$ . Para determinar $\vec{\omega}_{21}$ necesitamos la velocidad en otro punto. Para ello vamos a expresar la posición del otro extremo de la varilla en la base de la escuadra $O 1 X 1 Y 1$ . El punto $O$ se mueve siempre a lo largo del eje $O 1 X 1$ . Por trigonometría tenemos

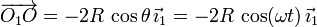
$\overrightarrow{O_1O} = -2R\,\cos\theta\,\vec{\imath}_1=-2R\,\cos(\omega t)\,\vec{\imath}_1$

De nuevo podemos derivar esta expresión para calcular 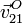$\vec{v}_{21}^O$

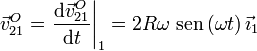
$\vec{v}_{21}^O=\left.\dfrac{\mathrm{d}\vec{v}_{21}^O}{\mathrm{d}t}\right|_1=2R\omega\,\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1$

Teniendo en cuenta que 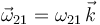$\vec{\omega}_{21}=\omega_{21}\,\vec{k}$ , la ecuación del campo de velocidades nos permite plantear la ecuación

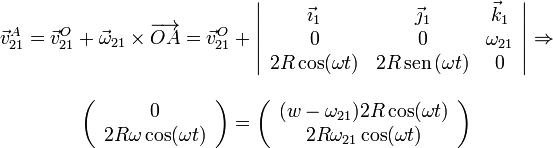
$\begin{array}{c} \vec{v}_{21}^A=\vec{v}_{21}^O+\vec{\omega}_{21}\times\overrightarrow{OA}= \vec{v}_{21}^O+ \left| \begin{array}{ccc} \vec{\imath}_1&\vec{\jmath}_1&\vec{k}_1\\0&0&\omega_{21}\\2R\cos(\omega t)&2R\,\mathrm{sen}\,(\omega t)&0 \end{array} \right|\Rightarrow\\ \\ \left( \begin{array}{c} 0\\2R\omega\cos(\omega t) \end{array} \right)= \left( \begin{array}{c} (w-\omega_{21})2R\cos(\omega t)\\2R\omega_{21}\cos(\omega t) \end{array} \right) \end{array}$

Por tanto $ω 21 = ω$ y la reducción en el punto $O$ es

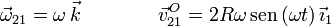
$\vec{\omega}_{21}=\omega\,\vec{k}\qquad\qquad\vec{v}_{21}^O=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1$

2.2.2 Movimiento {01}

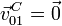El disco rueda sin deslizar sobre la línea $y 1 = - R$ . Por tanto el punto de contacto es el CIR y su velocidad en este movimiento es nula, $\vec{v}_{01}^C=\vec{0}$ . Por otro lado, aún no podemos determinar la velocidad angular de este movimiento. Por tanto lo que sabemos por ahora es

$\vec{\omega}_{01}=\omega_{01}\,\vec{k}\qquad\qquad\vec{v}_{01}^C=\vec{0}$

2.2.3 Movimiento {20}

El punto $O$ pertenece tanto al sólido "2" como al "0". Por tanto es un punto fijo en este movimiento. La reducción en $O$ es

$\vec{\omega}_{20}=\omega_{20}\,\vec{k}\qquad\qquad\vec{v}_{20}^O=\vec{0}$

2.2.4 Composición {21} = {20} + {01}

La velocidad 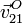$\vec{v}_{21}^O$ puede escribirse

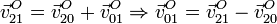
$\vec{v}_{21}^O=\vec{v}_{20}^O+\vec{v}_{01}^O\Rightarrow \vec{v}_{01}^O=\vec{v}_{21}^O-\vec{v}_{20}^O$

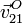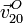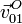
donde $\vec{v}_{21}^O$ y $\vec{v}_{20}^O$ son conocidas. Ahora podemos calcular $\vec{v}_{01}^O$

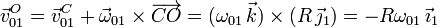
$\vec{v}_{01}^O=\vec{v}_{01}^C+\vec{\omega}_{01}\times\overrightarrow{CO}=(\omega_{01}\,\vec{k})\times(R\,\vec{\jmath}_1)=-R\omega_{01}\,\vec{\imath}_1$

Sustituyendo tenemos

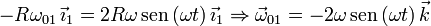
$-R\omega_{01}\,\vec{\imath}_1=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1 \Rightarrow \vec{\omega}_{01}=-2\omega\,\mathrm{sen}\,(\omega t)\,\vec{k}$

Para obtener $\vec{\omega}_{20}$ recurrimos a la composición de velocidades angulares

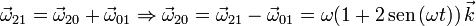
$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\Rightarrow\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=\omega(1+2\,\mathrm{sen}\,(\omega t))\,\vec{k}$

Por tanto, las reducciones pedidas son

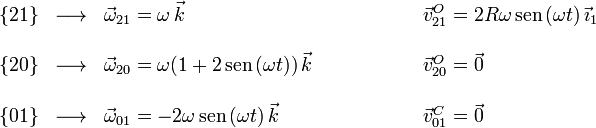
$\begin{array}{lclcl} \{21\}&\longrightarrow&\vec{\omega}_{21}=\omega\,\vec{k}&\qquad\qquad&\vec{v}_{21}^O=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1\\ &&&&\\ \{20\}&\longrightarrow&\vec{\omega}_{20}=\omega(1+2\,\mathrm{sen}\,(\omega t))\,\vec{k}&\qquad\qquad&\vec{v}_{20}^O=\vec{0}\\ &&&&\\ \{01\}&\longrightarrow&\vec{\omega}_{01}=-2\omega\,\mathrm{sen}\,(\omega t)\,\vec{k}&\qquad\qquad&\vec{v}_{01}^C=\vec{0} \end{array}$

2.3 Determinación del CIR del movimiento {21}

2.3.1 Gráfica

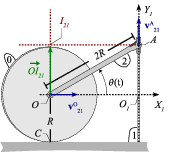
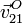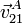Tenemos $\vec{v}_{21}^O$ y $\vec{v}_{21}^A$ . Si trazamos en cada punto la recta perpendicular a sus velocidades respectivas el punto de corte nos da $I 21$ , como se indica en el dibujo

2.3.2 Analítica

Partiendo de 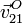$\vec{v}_{21}^O$ , la posición de $I 21$ es

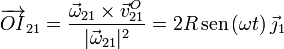
$\overrightarrow{OI}_{21} = \dfrac{\vec{\omega}_{21}\times\vec{v}_{21}^O}{|\vec{\omega}_{21}|^2}=2R\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}_1$

Podemos comprobar que ambos métodos dan el mismo resultado.

Disco articulado con una varilla (G.I.A.)

De Laplace

Revisión de 16:50 27 dic 2010

Contenido

1 Enunciado

2 Solución

2.1 Cálculo del vector de posición, velocidad y aceleración del punto A en el movimiento {21}

2.2 Reducciones cinemáticas de los movimientos

2.2.1 Movimiento {21}

2.2.2 Movimiento {01}

2.2.3 Movimiento {20}

2.2.4 Composición {21} = {20} + {01}

2.3 Determinación del CIR del movimiento {21}

2.3.1 Gráfica

2.3.2 Analítica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES