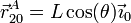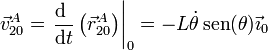5.6. Barra deslizante en armazón rotatorio
De Laplace
(→Movimiento de arrastre {01}) |
|||
| Línea 28: | Línea 28: | ||
<center><math>\vec{v}^A_{01}=(\dot{\varphi}\vec{k}_0)\times(L\cos(\theta)\vec{\imath}_0) = L\dot{\varphi}\cos(\theta)\vec{\jmath}_0</math></center> | <center><math>\vec{v}^A_{01}=(\dot{\varphi}\vec{k}_0)\times(L\cos(\theta)\vec{\imath}_0) = L\dot{\varphi}\cos(\theta)\vec{\jmath}_0</math></center> | ||
| + | ===Movimiento relativo {20}=== | ||
| + | El punto A de la barra se desliza a lo largo del eje <math>OX_0</math>. Puesto que conocemos su posición en todo momento, podemos hallar su velocidad simplemente derivando | ||
| + | |||
| + | <center><math>\vec{r}^A_{20}=L\cos(\theta)\vec{\imath}_0</math>{{tose}}<math>\vec{v}^A_{20}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\vec{r}^A_{20}\right)\right|_0=-L\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}_0</math></center> | ||
==Velocidades de B== | ==Velocidades de B== | ||
==Aceleraciones== | ==Aceleraciones== | ||
[[Categoría:Problemas de movimiento relativo (G.I.T.I.)]] | [[Categoría:Problemas de movimiento relativo (G.I.T.I.)]] | ||
Revisión de 12:18 28 nov 2010
Contenido |
1 Enunciado
El armazón de barras paralelas a los ejes OX0 y OZ0 (sólido “0”) rota alrededor del eje vertical fijo OZ1, de tal modo que el eje OX0 permanece siempre contenido en el plano horizontal fijo OX1Y1 (sólido “1”). Por otra parte, la varilla AB (sólido “2”), de longitud L, se mueve de forma que su extremo A desliza a lo largo del eje OX0, mientras que su extremo B desliza a lo largo del eje OZ0. Utilizando los ángulos θ y 
(definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine:
-
, 
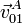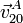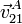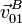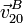y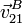 
.
-
, 
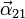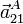y 
.
-
, 
y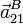 
.
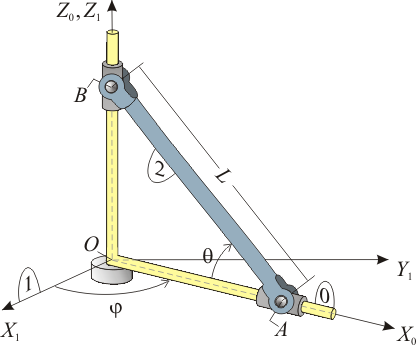
Nota: Se recomienda el uso de la base vectorial asociada al triedro “0” para resolver el ejercicio.
2 Velocidades de A
2.1 Movimiento de arrastre {01}
En su movimiento como punto del armazón, el punto A se encuentra rotando alrededor del eje OZ0. Su velocidad instantánea es
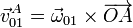
La velocidad angular de este movimiento la da la derivada temporal del ángulo que forman los dos ejes OX1 y OX0
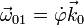
mientras que la posición instantánea de A es
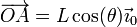
lo que nos da la velocidad de arrastre
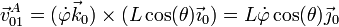
2.2 Movimiento relativo {20}
El punto A de la barra se desliza a lo largo del eje OX0. Puesto que conocemos su posición en todo momento, podemos hallar su velocidad simplemente derivando
