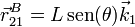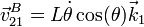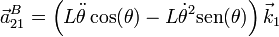5.6. Barra deslizante en armazón rotatorio
De Laplace
Contenido |
1 Enunciado
El armazón de barras paralelas a los ejes OX0 y OZ0 (sólido “0”) rota alrededor del eje vertical fijo OZ1, de tal modo que el eje OX0 permanece siempre contenido en el plano horizontal fijo OX1Y1 (sólido “1”). Por otra parte, la varilla AB (sólido “2”), de longitud L, se mueve de forma que su extremo A desliza a lo largo del eje OX0, mientras que su extremo B desliza a lo largo del eje OZ0. Utilizando los ángulos θ y  (definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine:
(definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine:
-
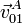 ,
, 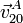 y
y 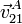 .
.
-
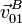 ,
, 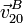 y
y 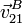 .
.
-
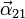 ,
, 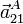 y
y 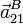 .
.
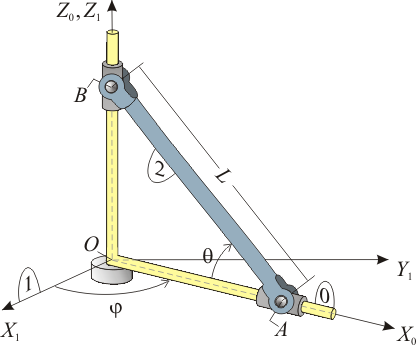
Nota: Se recomienda el uso de la base vectorial asociada al triedro “0” para resolver el ejercicio.
2 Velocidades de A
- Movimiento de arrastre {01}
- En su movimiento como punto del armazón, el punto A se encuentra rotando alrededor del eje OZ0. Su velocidad instantánea es
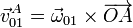
- La velocidad angular de este movimiento la da la derivada temporal del ángulo que forman los dos ejes OX1 y OX0
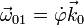
- mientras que la posición instantánea de A es
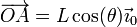
- lo que nos da la velocidad de arrastre
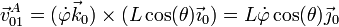
- Movimiento relativo {20}
- El punto A de la barra se desliza a lo largo del eje OX0. Puesto que conocemos su posición en todo momento, podemos hallar su velocidad simplemente derivando
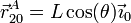

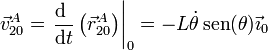
- Movimiento absoluto {21}
- Una vez que tenemos las velocidades de arrastre y relativa, la velocidad absoluta la calculamos sumando las dos anteriores
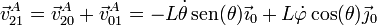
3 Velocidades de B
Las velocidades de B son incluso más fáciles de calcular que las de A.
- Velocidad de arrastre {01}
- El punto B se encuentra en el propio eje (permanente) de rotación, por lo que
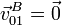
- Velocidad relativa {20}
- De nuevo se trata de un deslizamiento, que podemos hallar derivando la posición
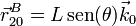

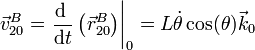
- Velocidad absoluta {21}
- Al ser nula la velocidad de arrastre, la absoluta coincide con la relativa
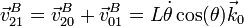
4 Aceleraciones
4.1 Aceleración angular
Para hallar la aceleración angular absoluta emplearemos la fórmula de composición de aceleraciones angulares
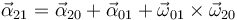
En el movimiento de arrastre tenemos una rotación en torno a un eje permanente de rotación, con velocidad angular dada por
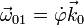
La aceleración angular de este movimiento es la derivada temporal de esta velocidad, calculada en el sistema 1. Este valor coincide con el calculado en el sistema 0 ya que el vector  es el mismo para los dos sistemas en todo instante
es el mismo para los dos sistemas en todo instante 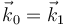
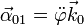
En realidad, el resultado es más general y la derivada de una velocidad angular  calculada en el sistema 0 coincide siempre con la hallada en el sistema 1:
calculada en el sistema 0 coincide siempre con la hallada en el sistema 1:
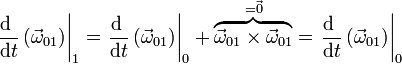
Para el movimiento relativo, el cálculo es similar. La velocidad angular la da la variación del ángulo θ que forman de manera continua la barra horizontal del armazón “0” y la barra “2”. La dirección y el sentido de  los da la regla de la mano derecha, observando para donde gira la barra “2” cuando θ aumenta
los da la regla de la mano derecha, observando para donde gira la barra “2” cuando θ aumenta
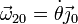
Derivando aquí respecto al tiempo en el sistema “0” obtenemos la aceleración angular relativa
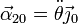
La aceleración angular absoluta la obtenemos sustituyendo en la fórmula de composición de aceleraciones
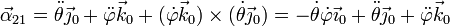
4.2 Aceleración de A
El teorema de Coriolis nos da la aceleración angular absoluta
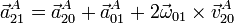
Veamos cada término por separado:
- Aceleración relativa {20}
- Puesto que conocemos el movimiento de A sobre la barra, podemos calcular la aceleración de A derivando su velocidad relativa
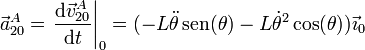
- Aceleración de arrastre {01}
- Al tratarse de una rotación permanente en torno a un eje que pasa por O
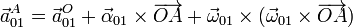
- donde
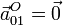
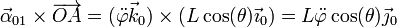
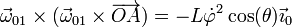
- lo que da la aceleración de arrastre
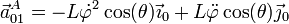
- Término de Coriolis
- Por último tenemos
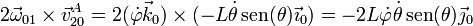
Sumando las tres contribuciones obtenemos la aceleración absoluta
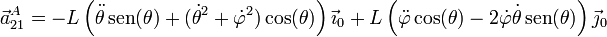
4.3 Aceleración de B
La aceleración absoluta de B es más sencilla de calcular que la de A. El teorema de Coriolis nos da
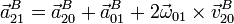
Sin embargo, la aceleración de arrastre de B es nula, por encontrarse este punto sobre un eje permanente de rotación. Además, la velocidad relativa 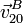 es a lo largo del eje Z y por tanto paralela a la velocidad angular
es a lo largo del eje Z y por tanto paralela a la velocidad angular  , por lo que también el término de Coriolis se anula y la aceleración absoluta coincide con la relativa.
, por lo que también el término de Coriolis se anula y la aceleración absoluta coincide con la relativa.
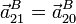
A su vez, la aceleración relativa se calcula derivando la velocidad, pues conocemos la posición de B en todo momento
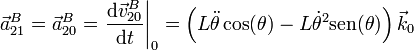
También podíamos haber dicho directamente que conocemos la posición de B en el sistema 1 y derivar esta expresión respecto al tiempo