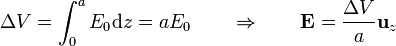Resistor conectado a generador real
De Laplace
(→Campo y corriente) |
|||
| Línea 19: | Línea 19: | ||
Si despreciamos los efectos de borde y suponemos el campo con componente en la dirección normal a las placas | Si despreciamos los efectos de borde y suponemos el campo con componente en la dirección normal a las placas | ||
| - | <center><math><math>\mathbf{E}=E\mathbf{u}_z\qquad\qquad\\mathbf{J}=\sigma E\mathbf{u}_z</math></center> | + | <center><math><math>\mathbf{E}=E\mathbf{u}_z\qquad\qquad\mathbf{J}=\sigma E\mathbf{u}_z</math></center> |
| + | |||
| + | Las ecuaciones anteriores conducen a que el campo eléctrico y la densidad de corriente son uniformes entre las placas. | ||
| + | |||
| + | <center><math><math>\mathbf{E}=E_0\mathbf{u}_z\qquad\qquad\mathbf{J}=J_0\mathbf{u}_z=\sigma E_0\mathbf{u}_z</math></center> | ||
| + | |||
| + | El valor de la componente E_0 se relaciona con la d.d.p. a través de la relación | ||
| + | |||
| + | <center><math>\Delta V = \int_0^a E_0\mathrm{d}z=aE_0\qquad\Rightarrow\qquad \mathbf{E}=\frac{\Delta V}{a}\mathbf{u}_z</math></center> | ||
| + | |||
==Potencia disipada== | ==Potencia disipada== | ||
==Energía almacenada== | ==Energía almacenada== | ||
==Campo magnético== | ==Campo magnético== | ||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
Revisión de 21:25 27 nov 2010
Contenido |
1 Enunciado
El espacio entre dos placas conductoras circulares, planas y paralelas de radio b, separadas una distancia a, se encuentra lleno de un material de permitividad 
, conductividad σ y permeabilidad μ0. Las placas se encuentran conectadas a un generador real de f.e.m. V0 y resistencia interna r. En el estado estacionario, determine
- La densidad de corriente y el campo eléctrico en el espacio entre las placas. Desprecie los efectos de borde.
- La potencia total disipada en el volumen entre las placas. ¿Para qué valor de la conductividad es máxima esta potencia disipada?
- La energía eléctrica almacenada en el material.
- Sabiendo que el campo magnético entre las placas es acimutal y dependiente sólo de la distancia al eje, calcule el valor de este campo magnético.
2 Campo y corriente
Al ser las placas perfectamente conductoras y encontrarse el sistema en un estado estacionario, existe una diferencia de potencial constante entre las placas. Sea ΔV esta d.d.p., considerando como placa a menor potencial la conectada al polo negativo de la fuente. Este voltaje no coincide con la f.e.m. de la fuente, debido a la caída de tensión en la resistencia interna. Se cumple que
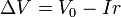
y no conoceremos ΔV hasta que hallemos la intensidad que circula por el sistema.
Suponiendo un valor dado para ΔV (que hallaremos más tarde), el cálculo del campo eléctrico y la densidad de corriente es inmediato. Las ecuaciones que se cumplen son
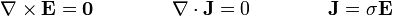
Si despreciamos los efectos de borde y suponemos el campo con componente en la dirección normal a las placas
Las ecuaciones anteriores conducen a que el campo eléctrico y la densidad de corriente son uniformes entre las placas.
El valor de la componente E_0 se relaciona con la d.d.p. a través de la relación
