Coordenadas esféricas. Líneas y superficies coordenadas
De Laplace
(Diferencias entre revisiones)
(→Líneas coordenadas) |
(→Líneas coordenadas) |
||
| Línea 3: | Línea 3: | ||
* Para la coordenada <math>\varphi</math> obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los ''paralelos''. | * Para la coordenada <math>\varphi</math> obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los ''paralelos''. | ||
| - | * Al variar <math>\theta\,</math> modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los ''meridianos''). Son semicircunferencias | + | * Al variar <math>\theta\,</math> modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los ''meridianos''). Son semicircunferencias y no circunferencias completas porque la colatitud solo llega hasta <math>\pi\,</math>. |
* Al alejarnos o acercarnos al origen de coordenadas, variando <math>r\,</math>, nos movemos sobre una semirrecta (''no'' una recta) que, partiendo del origen de coordenadas, pasa por el punto <math>P\,</math>. | * Al alejarnos o acercarnos al origen de coordenadas, variando <math>r\,</math>, nos movemos sobre una semirrecta (''no'' una recta) que, partiendo del origen de coordenadas, pasa por el punto <math>P\,</math>. | ||
Revisión de 10:14 20 nov 2007
Contenido |
1 Líneas coordenadas
- Para la coordenada
 obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los paralelos.
obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los paralelos.
- Al variar
 modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los meridianos). Son semicircunferencias y no circunferencias completas porque la colatitud solo llega hasta
modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los meridianos). Son semicircunferencias y no circunferencias completas porque la colatitud solo llega hasta 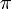 .
.
- Al alejarnos o acercarnos al origen de coordenadas, variando
 , nos movemos sobre una semirrecta (no una recta) que, partiendo del origen de coordenadas, pasa por el punto
, nos movemos sobre una semirrecta (no una recta) que, partiendo del origen de coordenadas, pasa por el punto  .
.
2 Superficies coordenadas
3 Artículo siguiente
Resumen de líneas y superficies coordenadas
4 Artículo anterior
Coordenadas cilíndricas. Líneas y superficies coordenadas







