Coordenadas esféricas. Líneas y superficies coordenadas
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Líneas coordenadas== ==Superficies coordenadas== ==Artículo siguiente== Resumen de líneas y superficies coordenadas ==Artículo anterior== [[Coordenadas cilíndricas. Lín...) |
(→Líneas coordenadas) |
||
| Línea 1: | Línea 1: | ||
==Líneas coordenadas== | ==Líneas coordenadas== | ||
| + | [[Imagen:esf-lin.png|left]] | ||
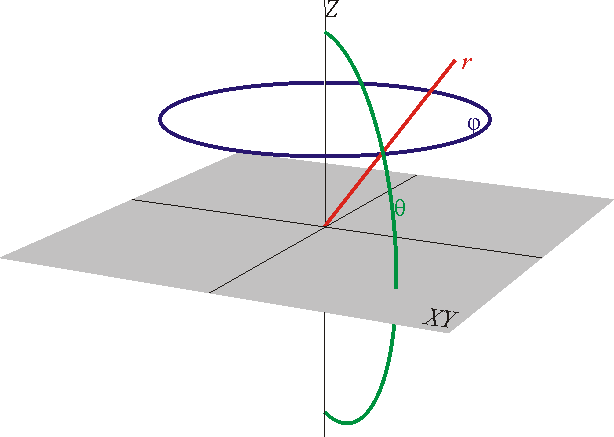
| + | * Para la coordenada <math>\varphi</math> obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los ''paralelos''. | ||
| + | |||
| + | * Al variar <math>\theta\,</math> modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los ''meridianos''). Son semicircunferencias verticales porque la colatitud solo llega hasta <math>\pi\,</math>. | ||
| + | |||
| + | * Al alejarnos o acercarnos al origen de coordenadas, variando <math>r\,</math>, nos movemos sobre una semirrecta (''no'' una recta) que, partiendo del origen de coordenadas, pasa por el punto <math>P\,</math>. | ||
==Superficies coordenadas== | ==Superficies coordenadas== | ||
Revisión de 10:42 20 nov 2007
Contenido |
1 Líneas coordenadas
- Para la coordenada
obtenemos, de nuevo circunferencias horizontales, lo que en la superficie terrestre corresponde a los paralelos.
- Al variar
modificamos la latitud en la superficie esférica, por lo que resultan semicircunferencias verticales (los meridianos). Son semicircunferencias verticales porque la colatitud solo llega hasta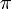 
.
- Al alejarnos o acercarnos al origen de coordenadas, variando
, nos movemos sobre una semirrecta (no una recta) que, partiendo del origen de coordenadas, pasa por el punto 
.
2 Superficies coordenadas
3 Artículo siguiente
Resumen de líneas y superficies coordenadas
4 Artículo anterior
Coordenadas cilíndricas. Líneas y superficies coordenadas
