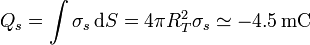Entrar Página Discusión Historial Go to the site toolbox

Corrientes atmosféricas

De Laplace

(Diferencias entre revisiones)
(→Diferencia de potencial entre la superficie y la ionosfera)
(→Distribución de cargas)
Línea 72: Línea 72:
===Distribución de cargas===
===Distribución de cargas===
 +
La distribución de cargas es inmediata a partir del campo eléctrico
 +
 +
<center><math>\rho=\varepsilon_0\nabla{\cdot}\mathbf{E}=\varepsilon_0\frac{\mathrm{d}E}{\mathrm{d}z}=-\sum_i(\varepsilon_0
 +
E_i\alpha_i)\mathrm{e}^{-\alpha_iz}
 +
</math></center>
 +
 +
La mayor concentración de cargas se da junto la superficie terrestre y vale
 +
 +
<center><math>\rho(z=0)=2.6\times 10^{-12}\,\frac{\mathrm{C}}{\mathrm{m}^3}</math></center>
 +
 +
Esta densidad de carga disminuye rápidamente con la altura. A 100 m se ha reducido a la mitad y a 1 km es la centésima parte de su valor en la superficie.
 +
 +
Sobre la superficie habrá una densidad de carga igual al salto en la componente normal del vector desplazamiento
 +
 +
<center><math>\sigma_s=\mathbf{n}{\cdot}[\mathbf{D}]=\varepsilon_0 E_0=-8.9\times 10^{-10}\frac{\mathrm{C}}{\mathrm{m}^2}</math></center>
 +
 +
lo que supone una carga total en la superficie de la Tierra
 +
 +
<center><math>Q_s=\int \sigma_s \,\mathrm{d}S=4\pi R_T^2\sigma_s\simeq
 +
-4.5\,\mathrm{mC}</math></center>
 +
===Corriente que llega a la superficie===
===Corriente que llega a la superficie===
===Potencia disipada en la atmósfera===
===Potencia disipada en la atmósfera===

Revisión de 15:43 12 jun 2008

Contenido

1 Enunciado

La resistividad del aire en la atmósfera decrece exponencialmente con la altura como

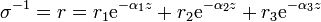
\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ r_2 \mathrm{e}^{-\alpha_2 z}+r_3 \mathrm{e}^{-\alpha_3 z}\,

donde

\begin{array}{|c|c|c|} \hline i & r_i\ (10^{12}\,\Omega{\cdot}{\rm m}) & \alpha_i ({\rm km}^{-1}) \\ \hline \hline 1 & 46.9 & 4.527\\ \hline 2 & 22.2 & 0.375 \\ \hline 3 & 5.9 & 0.121 \\\hline \end{array}

El campo eléctrico en zonas despejadas de la superficie de la Tierra vale 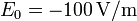E_0=-100\,\mathrm{V}/\mathrm{m}. Este campo es prácticamente constante y va siempre en la dirección vertical.

A partir de estos datos halle

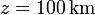  1. El valor del campo eléctrico para un punto situado entre la superficie de la Tierra y la ionosfera (z = 100\,\mathrm{km}).
  2. La diferencia de potencial entre la superficie y la ionosfera.
  3. La distribución de cargas en la atmósfera.
  4. La corriente total que llega a la superficie de la Tierra.
  5. La potencia necesaria para mantener esta corriente estacionaria
  6. Estime el tiempo que tardaría la atmósfera en descargarse si no existiera un mecanismo generador

2 Solución

2.1 Campo eléctrico en el aire

Si el estado es estacionario se cumplirá que

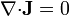
\nabla{\cdot}\mathbf{J}=0

Si además consideramos que la dirección de la densidad de corriente es perpendicular al suelo (que es un conductor perfecto), nos queda 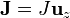\mathbf{J}=J\mathbf{u}_{z}, y la ecuación anterior se reduce a

\frac{\partial{}J}{\partial{}z}=0    \Rightarrow    J = J0 = cte

La densidad de corriente es uniforme. A partir de este dato podemos obtener el campo en cualquier punto de la atmósfera

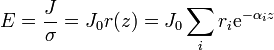
E=\frac{J}{\sigma}=J_0r(z)=J_0\sum_ir_i\mathrm{e}^{-\alpha_iz}

El valor de J0 lo sacamos del valor del campo y de la resistividad en la superficie

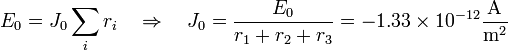
E_0=J_0\sum_ir_i\quad\Rightarrow\quad J_0=\frac{E_0}{r_1+r_2+r_3}= -1.33\times 10^{-12} \frac{\mathrm{A}}{\mathrm{m}^2}

El campo en función de la altura queda entonces

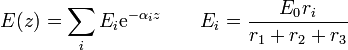
E(z)=\sum_i E_i \mathrm{e}^{-\alpha_i z}\qquad E_i= \frac{E_0r_i}{r_1+r_2+r_3}

Los valores de los coeficientes son

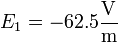
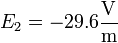
E_1=-62.5\frac{\mathrm{V}}{\mathrm{m}}    E_2=-29.6\frac{\mathrm{V}}{\mathrm{m}}    E_3=-7.9\frac{\mathrm{V}}{\mathrm{m}}

Según esto, la principal contribución al campo es la que decae más rápidamente.

2.2 Diferencia de potencial entre la superficie y la ionosfera

La diferencia de potencial la obtenemos integrando el campo eléctrico entre el suelo y la ionosfera

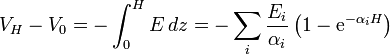
V_H-V_0=-\int_{0}^{H}E\,dz=-\sum_i \frac{E_i}{\alpha_i}\left(1-\mathrm{e}^{-\alpha_iH}\right)

Para todas las exponenciales el valor $\alpha_iH$ es tan grande que podemos despreciar la exponencial correspondiente, resultando la expresión para el potencial

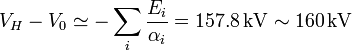
V_H-V_0\simeq -\sum_i\frac{E_i}{\alpha_i}= 157.8\,\mathrm{kV}\sim 160\,\mathrm{kV}

Experimentalmente se comprueba que este valor puede fluctuar notablemente y suele llegar hasta los 200 kV.

2.3 Distribución de cargas

La distribución de cargas es inmediata a partir del campo eléctrico

\rho=\varepsilon_0\nabla{\cdot}\mathbf{E}=\varepsilon_0\frac{\mathrm{d}E}{\mathrm{d}z}=-\sum_i(\varepsilon_0 E_i\alpha_i)\mathrm{e}^{-\alpha_iz}

La mayor concentración de cargas se da junto la superficie terrestre y vale

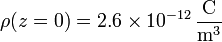
\rho(z=0)=2.6\times 10^{-12}\,\frac{\mathrm{C}}{\mathrm{m}^3}

Esta densidad de carga disminuye rápidamente con la altura. A 100 m se ha reducido a la mitad y a 1 km es la centésima parte de su valor en la superficie.

Sobre la superficie habrá una densidad de carga igual al salto en la componente normal del vector desplazamiento

\sigma_s=\mathbf{n}{\cdot}[\mathbf{D}]=\varepsilon_0 E_0=-8.9\times 10^{-10}\frac{\mathrm{C}}{\mathrm{m}^2}

lo que supone una carga total en la superficie de la Tierra

Q_s=\int \sigma_s \,\mathrm{d}S=4\pi R_T^2\sigma_s\simeq -4.5\,\mathrm{mC}

2.4 Corriente que llega a la superficie

2.5 Potencia disipada en la atmósfera

2.6 Tiempo de descarga atmósferica

Obtenido de "http://tesla.us.es/wiki/index.php/Corrientes_atmosf%C3%A9ricas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace