Corrientes atmosféricas
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Nueva página: ==Enunciado== La resistividad del aire en la atmósfera decrece exponencialmente con la altura como <center><math>\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ r_2 \mathrm{e}^{-\alpha_...)
Edición más nueva →
(Nueva página: ==Enunciado== La resistividad del aire en la atmósfera decrece exponencialmente con la altura como <center><math>\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ r_2 \mathrm{e}^{-\alpha_...)
Edición más nueva →
Revisión de 16:35 12 jun 2008
Contenido |
1 Enunciado
La resistividad del aire en la atmósfera decrece exponencialmente con la altura como
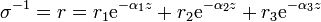
donde
El campo eléctrico en zonas despejadas de la superficie de la Tierra vale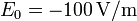 
. Este campo es prácticamente constante y va siempre en la dirección vertical.
A partir de estos datos halle
- El valor del campo eléctrico para un punto situado entre la superficie de la Tierra y la ionosfera (
).
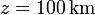- La diferencia de potencial entre la superficie y la ionosfera.
- La distribución de cargas en la atmósfera.
- La corriente total que llega a la superficie de la Tierra.
- La potencia necesaria para mantener esta corriente estacionaria
- Estime el tiempo que tardaría la atmósfera en descargarse si no existiera un mecanismo generador
