1.3. Fórmulas dimensionalmente incorrectas
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Teniendo en cuenta las dimensiones calculadas en el problema anterior, indique cuáles de las siguientes expresiones son necesariamente incorrectas: :a) <math>W =…') |
(→Caso (a)) |
||
| Línea 17: | Línea 17: | ||
Para que una fórmula sea dimensionalmente correcta los dos miembros de la ecuación deben tener las mismas dimensiones, y lo mismo debe ocurrir con cada uno de los sumandos de las sumas o diferencias que aparezcan en ella. | Para que una fórmula sea dimensionalmente correcta los dos miembros de la ecuación deben tener las mismas dimensiones, y lo mismo debe ocurrir con cada uno de los sumandos de las sumas o diferencias que aparezcan en ella. | ||
| - | En el primer caso tenemos que el trabajo tiene dimensiones de [[Ejemplos_de_análisis_dimensional#Trabajo|masa por velocidad al cuadrado]] | + | En el primer caso |
| + | |||
| + | |||
| + | tenemos que el trabajo tiene dimensiones de [[Ejemplos_de_análisis_dimensional#Trabajo|masa por velocidad al cuadrado]] | ||
<center><math>[W]= M L^2T^{-2}\,</math></center> | <center><math>[W]= M L^2T^{-2}\,</math></center> | ||
| + | De los términos del segundo miembro, el primero tiene claramente las mismas dimensiones que este | ||
| + | |||
| + | \left[\frac{1}{2}mv^2\right] | ||
==Caso (b)== | ==Caso (b)== | ||
Revisión de 17:38 8 sep 2010
Contenido |
1 Enunciado
Teniendo en cuenta las dimensiones calculadas en el problema anterior, indique cuáles de las siguientes expresiones son necesariamente incorrectas:
- a)
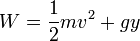
- b)
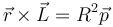
- c)
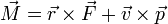
- d)
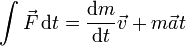
- e)
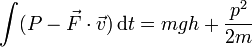
- f)
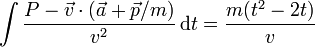
2 Caso (a)
Para que una fórmula sea dimensionalmente correcta los dos miembros de la ecuación deben tener las mismas dimensiones, y lo mismo debe ocurrir con cada uno de los sumandos de las sumas o diferencias que aparezcan en ella.
En el primer caso
tenemos que el trabajo tiene dimensiones de masa por velocidad al cuadrado
![[W]= M L^2T^{-2}\,](/wiki/images/math/9/7/e/97e5c25fc7da2c830e34ba663f3a050e.png)
De los términos del segundo miembro, el primero tiene claramente las mismas dimensiones que este
\left[\frac{1}{2}mv^2\right]





