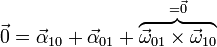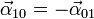Movimiento relativo (G.I.T.I.)

De Laplace

Revisión de 12:18 15 ago 2010

1 Introducción

Cuando se estudia el movimiento de un único sólido rígido se tiene la expresión general para el campo de velocidades

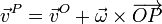
que nos dice que podemos conocer la velocidad de cada punto conocidos 6 datos: las 3 componentes del vector velocidad angular y las 3 componentes de un punto arbitrario que tomamos como origen de coordenadas.

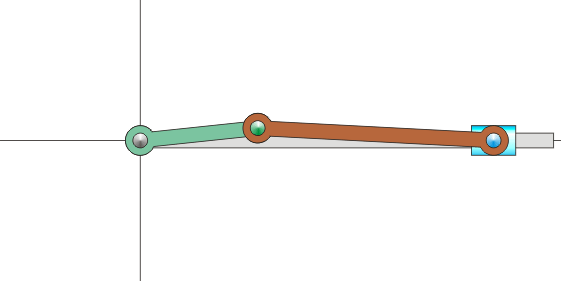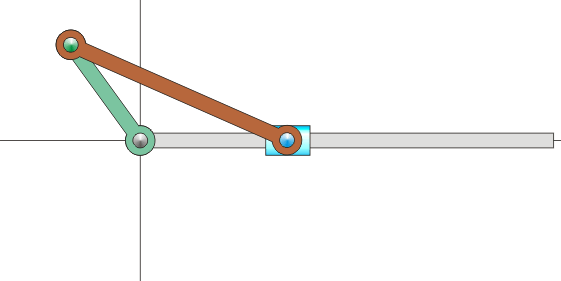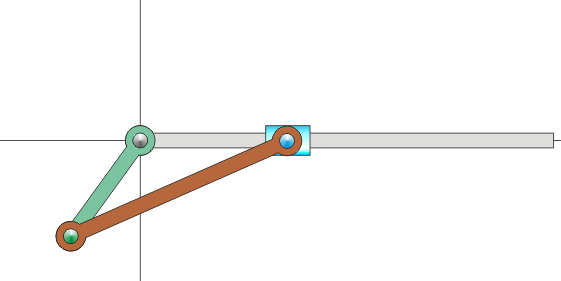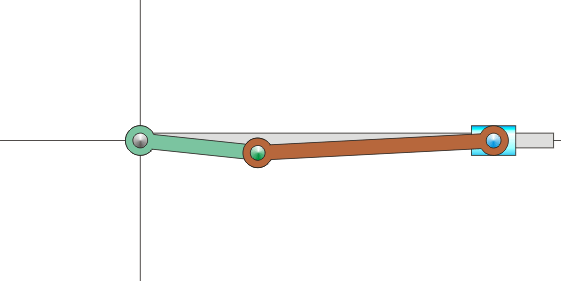
Sin embargo, en muchas situaciones, ni la velocidad angular ni la velocidad de O son datos inmediatos. Por ejemplo, consideremos el mecanismo sencillo de una biela y una manivela, como los que se encuentran dentro de un motor de explosión. Está formado por dos barras. Una, la manivela, gira en torno a uno de sus extremos, unido a un punto fijo. La segunda, la biela, tiene uno de sus extremos articulado al extremo móvil de la manivela, mientras que el otro está obligado a moverse en línea recta.

Es claro que, respecto a un sistema fijo, la manivela efectúa un movimiento de rotación, pero ¿qué movimiento realiza la biela en este mismo sistema? No es evidente de entrada, pues se desplaza a la vez que gira. Lo que sí sabemos es que, vista desde la manivela, la biela está girando respecto a su extremo.

Se trata entonces de hacer una composición de movimientos. El movimiento de la biela lo podemos describir como una rotación en torno a un extremo de la manivela, que a la vez gira en torno a su otro extremo respecto al sistema fijo.

Un ejemplo tridimensional lo representa un cono que rueda sobre un plano. Podemos ver este movimiento como una rotación instantánea en torno a la recta de contacto entre el cono y el plano (pues los puntos de contacto tienen velocidad nula y forman el EIR) pero también puede verse como una composición de dos rotaciones, una en torno a un eje vertical y otra en torno al eje del cono.

En este tema veremos el tratamiento matemático de la descripción de movimientos de sólidos en varios sistemas de referencia simultáneos (movimientos relativos), así como la composición de dos o más movimientos rígidos para dar lugar a un movimiento neto.

2 Notación y definiciones

2.1 Sólidos y sistemas de referencia

El primer paso para estudiar el movimiento reklativo consiste en generalizar el concepto de sólido rígido.

Normalmente, cuando uno piensa en un sólido rígido imagina un objeto amorfo, como una piedra, o moldeado, como una pieza de un mecanismo, pero en cualquier caso de tamaño finito. Cuando se habla de los puntos del sólido se piensa en los átomos que lo componen. No tendría sentido considerar punto del sólido a un lugar del espacio en el que no se encuentra el sólido en cuestión.

No obstante, tenemos una fórmula general para las velocidades del punto del sólido, que depende sólo de la posición del punto respecto a un cierto sistema de referencia, no de si en ese punto se encuentra una partícula material o no. Igualmente, la fórmula no requiere que se trate de un verdadero sólido rígido. Un sólido deformable, un líquido o un gas cuyos puntos se muevan según la fórmula anterior describe un movimiento rígido, aunque el medio material no sea indeformable.

Podemos abstraer entonces el concepto de sólido rígido como medio material, sino como un conjunto de puntos (que abarca todo el espacio), descrito por un cierto sistema de referencia, y tal que el campo de velocidades (y aceleraciones) es el correspondiente a un movimiento rígido

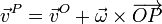
Si tenemos varios sólidos, a cada uno de ellos irá asociado un sistema de referencia y una distribución de velocidades para todos los puntos del espacio, independientemente de si forman parte del medio material o no. Es más, en la descripción de un problema parecen usualmente sólidos intermedios que no poseen existencia material alguna. Usaremos las expresiones "sólido" y "sistema de referencia" de manera sinónima.

Un punto P del espacio no pertenecerá entonces a un sólido en concreto, sino a todos ellos simultáneamente.

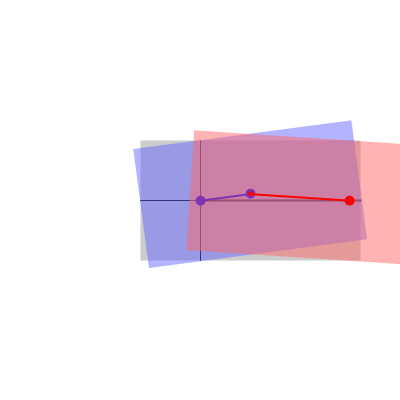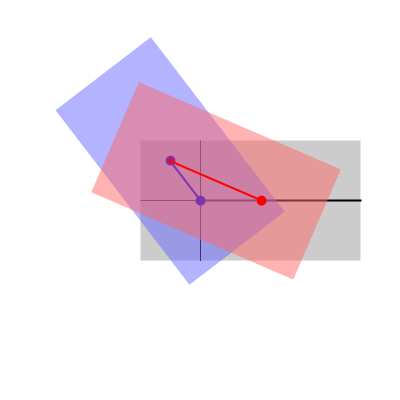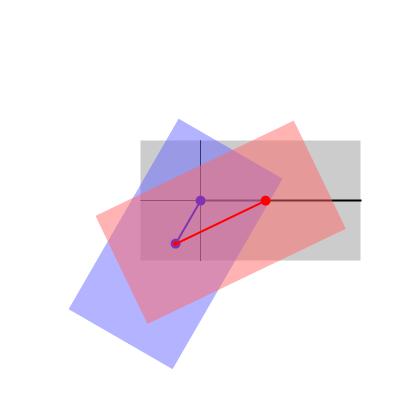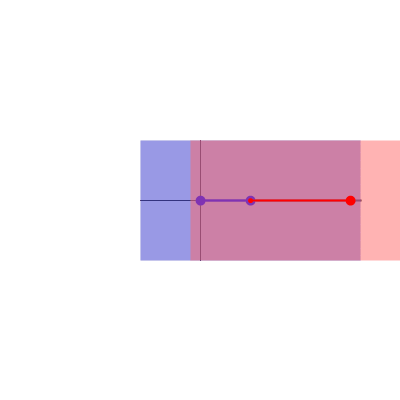
Para poder visualizar este concepto podemos volver al ejemplo del mecanismo biela-manivela. El movimiento de este sistema transcurre en un plano, por lo que podemos prescindir de la tercera coordenada. El sistema se compone de tres sólidos: la barra fija (sólido 1), la manivela (sólido 0) y la biela (sólido 2). A cada uno de ellos podemos asociar un sistema de referencia en un plano. Podemos imaginar estos sistemas de referencia como hojas de papel superpuestas. Habrá una hoja de papel pegada a la barra. Sobre ella una hoja de papel unida a la manivela y sobre ésta una tercera hoja unida a la biela. Cada hoja se extiende a todo el plano. En cada instante, cada hoja se mueve respecto a las otras dos, aunque sigan superpuestas.

Un punto P del plano lo podemos imaginar como un alfiler que, en un instante dado, atraviesa simultáneamente las tres hojas de papel, de forma que tenemos un agujero en cada uno de las hojas, por ello decimos que el punto P está en los tres sólidos, aunque tenga vectores de posición diferentes en cada uno.

Cuando los sólidos se mueven unos respecto a los otros, la posición del punto P puede permanecer fija en alguno de los sólidos, pero cambiar en los otros. El punto P tendrá velocidad nula en uno de los sistemas de referencia y distinta de cero en los otros dos. Habrá situaciones, como el punto de articulación de la biela y la manivela, que tendrá velocidad nula en estos los sólidos 0 y 2, pero que estará en movimiento respecto al sólido 1.

Observemos que podemos hallar el estado de movimiento de, por ejemplo, la articulación de la biela con la barra, considerando esta articulación como parte del sólido 0 (la manivela) pese a que físicamente este punto no forme parte de la manivela. Debemos imaginarnos unos ejes solidarios con la manivela que llegan hasta este punto y determinar cómo se mueve un punto fijo en este sistema de referencia cuando la manivela efectúa sus movimiento de rotación respecto a la barra (o respecto a la biela).

En un sistema tridimensional la idea es exactamente la misma, aunque en lugar de hojas de papel superpuestas deberíamos imaginar volúmenes coincidentes que se mueven de distinta manera. Dado que esta idea es difícil de concebir, nos conformaremos con dibujar sistemas de ejes en movimiento relativo, pero manteniendo siempre en mente que los sólidos no son solo los ejes, sino todo el espacio.

Según esto, la pregunta ¿cuál es la velocidad del punto P? no tiene sentido. La pregunta siempre debe ser ¿cuál es la velocidad del punto P, considerado como parte del sólido i, respecto al sólido k?

Denotaremos el estado de movimiento del sólido i respecto al sólido k (sólido observador) como

La velocidad de un punto de un sólido i respecto a un sistema de referencia ligado a otro sólido k la escribiremos

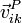
Igualmente, podremos definir la aceleración del punto P, como parte del sólido i respecto a un sistema de ejes fijo en el sólido k:

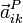
Haciendo una extensión del lenguaje, aplicaremos la misma notación para el vector de posición

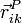
si bien este caso, el primer subíndice es superfluo, ya que el punto P no solo pertenece al sólido i, sino a todos los sólidos (incluyendo el k). Sin embargo, mantenemos la notación, para poder decir que

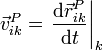
esto es, la velocidad de un punto de un sólido i respecto a otro k es igual a la derivada temporal del vector de posición de ese punto de i medido en el sólido k.

Puesto que cada uno de los sólidos presentes efectúa movimientos rígidos respecto a cualquiera de los restantes sólidos, también podremos definir la velocidad angular sel sólido i respecto al sólido k

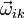
Esta velocidad angular no lleva superíndice pues no está asociada a ningún punto en concreto, sino que es un vector libre, válido para todo el sólido. Asimismo se define la aceleración angular del sólido i respecto al sólido k

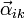
En el caso en que hay solo tres sólidos, son típicas los siguientes términos

Sólido fijo

El etiquetado como 1.

Sólido problema

El etiquetado como 2.

Sólido intermedio

El etiquetado como 0.

Movimiento absoluto

El del sólido problema respecto al fijo: {21}

Movimiento relativo

El del sólido problema respecto al sólido intermedio: {20}

Movimiento de arrastre

El del sólido intermedio respecto al fijo: {01}

3 Derivación en ejes móviles. Fórmulas de Poisson

El que la velocidad de un punto pueda ser cero en un sistema de referencia y no nula en otro muestra que la derivada respecto al tiempo depende del sistema de referencia, que debe ser indicado explícitamente.

Este problema no aparece con las derivadas de las cantidades escalares, cuyo valor es el mismo para todos los sistemas de referencia. El problema surge con las magnitudes vectoriales (y tensoriales, que no consideraremos) debido a que los propios vectores de la base son funciones del tiempo, al moverse un sistema de referencia respecto a otro.

3.1 Derivada temporal en una base

Definimos la derivada temporal de una magnitud vectorial 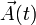en un sistema 1, como la que se obtiene, aplicando las reglas habituales de derivación, admitiendo que los vectores de la base permanecen constantes, esto es, si

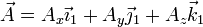
su derivada temporal en el sistema 1 es

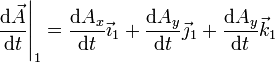
Nótese que las derivadas de las componentes, que son cantidades escalares, no precisan subíndice.

Definimos la velocidad y la aceleración de un punto P (que tomamos como perteneciente al sólido 2, aunque puede tratarse de una simple partícula material), tal como se miden en el sistema, y la aceleración angular del sólido 2 medida en el sistema 1, como

                

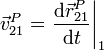
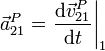
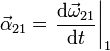
3.2 Relación entre derivadas temporales

Supongamos que tenemos una cierta cantidad vectorial 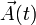de la que hemos calculado, en un isntante t_0, su derivada temporal en dos sistemas de referencia 0 y 1, y queremos relacionar estas dos cantidades. Supongamos que instantáneamente los ejes de coordenadas son coincidentes (pero no permanentemente, pues el sólido 0 se estará moviendo respecto al 1. Esto quiere decir que, en t = t₀

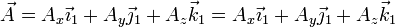
Si derivamos respecto al tiempo en el sistema 1

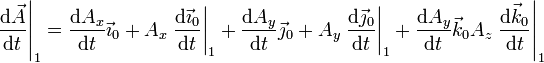
Necesitamos entonces conocer la derivada temporal de los vectores de la base. El vector unitario 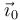es el que une al origen de coordenadas, O, con un punto A, situado a una distancia unidad a lo largo del eje X. Su derivada es

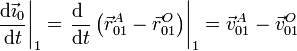
Aplicando la expresión del campo de velocidades de un sólido

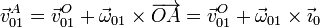
llegamos a

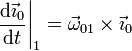
A este mismo resultado se llega directamente empleando la equiproyectividad del campo de velocidades y es justamente la propiedad que permite definir la velocidad angular del sólido, de acuerdo con la demostración del Teorema de Chasles.

Análogamente tenemos, para los otros dos vectores

        

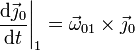
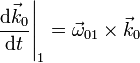
Estas tres igualdades se conocen como fórmulas de Poisson.

Sustituyendo y reordenando términos nos queda

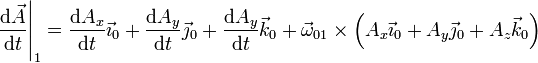
que equivale a

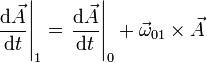
Esta igualdad también se conoce como fórmula de Poisson y contiene como casos particulares a las expresiones correspondientes a los vectores de la base.

Esta identidad es aplicable a cualquier magnitud vectorial, lo que incluye a las posiciones, velocidades y las propias velocidades angulares.

4 Composición de dos movimientos

4.1 Composición de velocidades

Una vez que disponemos de la fórmula de Poisson, podemos aplicarla para relacionar la velocidad de un punto, medida por dos observadores diferentes.

Supongamos un punto P, que se mueve con el sólido móvil 2, tal que su vector de posición respecto al origen O₁ de un sistema fijo 1 es

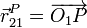
y respecto al origen O de un sólido intermedio 0 es

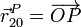
Estos dos vectores se relacionan por

      

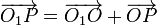
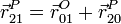
Derivando aquí respecto al tiempo en el sistema 1 llegamos a la relación (Demostración)

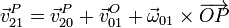
Si aquí sustituimos el campo de velocidades del sólido 0, la velocidad se reduce a

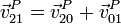
esto es la velocidad del punto P del sólido móvil, medida por el sólido fijo es la suma de la medida por el sólido intermedio más la que tendría el punto P, si perteneciera al sólido intermedia, medida en el sistema fijo.

En particular, si el sólido 2 es el mismo que el 1, el primer miembro se anula y llegamos a

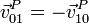
Hay que destacar que la expresión de la velocidad como suma de velocidades es una relación entre valores instantáneos de las diferentes cantidades, no como funciones del tiempo. Por tanto, no puede derivarse respecto al tiempo para hallar las aceleraciones. La razón es la siguiente: en la expresión aparece la velocidad del punto P del sólido 0, pero el punto P no es siempre el mismo punto material en el sólido 0, sino aquel que en cada instante coincide con el punto P del sólido 2 (que sí es un punto material), esto quiere decir que en el instante t empleamos la velocidad de un punto P, pero en el instante t + dt empleamos la velocidad de otro punto P diferente, y la diferencia de estas dos velocidades no da la aceleración de ninguno de los dos.

La expresión en términos de la velocidad de O y la velocidad angular, en cambio, si puede derivarse respecto al tiempo, ya que el punto O del sólido 0 si está perfectamente definido y se puede seguir su movimiento en el tiempo.

Una consecuencia de la ecuación anterior, y que parece ir contra el sentido común, es la siguiente. Supongamos que tenemos dos observadores A y B, pertenecientes a sólidos 1 y 2, respectivamente. En general, no se cumple que la velocidad de A medida por B sea opuesta a la de B medida por A

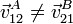
En este problema se analiza un ejemplo que muestra distintas variantes de esta desigualdad.

4.2 Composición de velocidades angulares

Una vez que tenemos la relación entre velocidades lineales, podemos hallar la de velocidades angulares. El resultado es que en tod instante (Demostración)

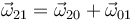
A diferencia de la ecuación para las velocidades, esta relación sí puede derivarse respecto al tiempo. La razón es que la velocidad angular es un vector libre que no depende de la posición de ningún punto en concreto, por lo que desaparece el problema de si el punto P en cada instante es el mismo o no.

4.3 Composición de aceleraciones. Teorema de Coriolis

Podemos relacionar las aceleraciones medidas por dos observadores a partir de la expresión

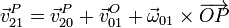
Derivando respecto al tiempo en el sistema 1 obtenemos,(Demostración)

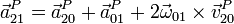
Este es el conocido como Teorema de Coriolis. Vemos que, a diferencia de la velocidad, la aceleración del movimiento absoluto no es la suma de la del movimiento relativo más la del de arrastre.

En el caso particular de que el sólido 2 y el 1 sean el mismo obtenemos

      

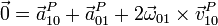
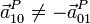
4.4 Composición de aceleraciones angulares

La ley para la composición de aceleraciones la obtenemos derivando la ley de composición de velocidades angulares

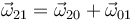
Derivando cada término resulta (Demostración)

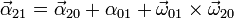
En el caso particular de que el sólido 2 y el 1 sean el mismo nos queda

      

5 Composición de N movimientos

5.1 Generalización de las fórmulas

5.2 Reducción de un sistema

5.3 Sistemas equivalentes