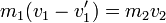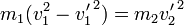Colisión de dos péndulos
De Laplace
(→Ecuaciones generales) |
(→Ecuaciones generales) |
||
| Línea 17: | Línea 17: | ||
La conservación de la energía cinética nos da | La conservación de la energía cinética nos da | ||
| - | <center><math>\frac{1}{2}m_1 v_1^2 = \frac{1}{2}m_1 {v'}^ | + | <center><math>\frac{1}{2}m_1 v_1^2 = \frac{1}{2}m_1 {v'_1}^2 + \frac{1}{2}m_2 {v'_2}^2</math></center> |
Operando en estas ecuaciónes, como en el problema de las colisiones de dos partículas obtenemos | Operando en estas ecuaciónes, como en el problema de las colisiones de dos partículas obtenemos | ||
| - | <center><math>m_1(v_1-v_1') = m_2v_2\,</math>{{qquad}}{{qquad}}<math>m_1(v_1^2-v'_1^2) = m_2 v'_2^2</math></center> | + | <center><math>m_1(v_1-v_1') = m_2v_2\,</math>{{qquad}}{{qquad}}<math>m_1(v_1^2-{v'_1}^2) = m_2 {v'_2}^2</math></center> |
==Caso ''m''<sub>1</sub> > ''m''<sub>2</sub>== | ==Caso ''m''<sub>1</sub> > ''m''<sub>2</sub>== | ||
Revisión de 19:28 22 jun 2010
Contenido |
1 Enunciado
Se tienen dos péndulos ideales con barras rígidas de la misma longitud L y masa nula, que cuelgan del mismo punto O. Las masas sujetas a los extremos de los hilos son respectivamente m1 y m2. La masa m1 es elevada a una altura h1 y se suelta desde el reposo, colisionando con la masa m2 que se encuentra en el punto más bajo.
Suponiendo que la colisión es elástica, determina la altura a la que sube cada masa tras la colisión. Distingue los casos m1 > m2, m1 = m2 y m1 < m2.
¿Qué condiciones deben cumplirse para conseguir que la masa m2 gire y llegue hasta arriba del todo?
2 Ecuaciones generales
La dinámica de este sistema es simple: la masa m1 desciende y golpea horizontalmente a la masa m2. Como resultado de la colisión, ambas adquieren una nueva velocidad, lo que las impulsa hacia arriba, ascendiendo hasta una cierta altura máxima. En ciertos casos, como veremos, una de ellas puede llegar a dar la vuelta completa.
En la colisión, por ser elástica, se conservan tanto la energía como el momento cinético. La conservación del momento cinético equivale en este caso, como en el del péndulo balístico, a la conservación de la cantidad de movimiento.
Al ser las velocidades inmediatamente antes y después de la colisión puramente horizontales, podemos escribir la conservación de la cantidad de movimiento en forma escalar, considerando solo la componente horizontal:
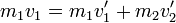
La conservación de la energía cinética nos da
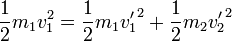
Operando en estas ecuaciónes, como en el problema de las colisiones de dos partículas obtenemos