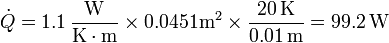Fusión de hielo en un recipiente
De Laplace
(→Enunciado) |
(→Flujo de calor) |
||
| Línea 13: | Línea 13: | ||
<center><math>\dot{Q}=k A\frac{\Delta T}{\Delta x}</math></center> | <center><math>\dot{Q}=k A\frac{\Delta T}{\Delta x}</math></center> | ||
| - | En este caso A es el área lateral del recipiente, | + | En este caso A es el área lateral del recipiente. Este área es la de la base, más la parte de cara lateral hasta la altura a la que llega el agua. hallamos primero esta altura |
| - | <center><math>\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times | + | <center><math>h = \frac{V}{\pi a^2}=\frac{1000\,\mathrm{cm}^3}{\pi (8\,\mathrm{cm})^2} = 4.97\,\mathrm{cm}</math></center> |
| + | |||
| + | Nótese que no hace falta distinguir entre agua e hielo, ya que por tratarse de la misma sustancia, el principio de Arquímedes nos dice que el volumen desalojado de agua por 0.5 kg de hielo es justamente 0.5 litros. | ||
| + | |||
| + | La superficie de agua en contacto con el vidrio es | ||
| + | |||
| + | <center><math>A = \pi r^2 + 2\pi r h = \pi r (2+h) = 0.0451\,\mathrm{m}^2</math></center> | ||
| + | |||
| + | En la expresión del flujo de calor <math>\Delta T</math> la diferencia de temperaturas entre las dos caras (20 K) y <math>\Delta x</math> el espesor del recipiente (0.01 m). Por tanto | ||
| + | |||
| + | <center><math>\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 0.0451\mathrm{m}^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 99.2\,\mathrm{W}</math></center> | ||
==Hielo fundido por segundo== | ==Hielo fundido por segundo== | ||
==Variación de entropía== | ==Variación de entropía== | ||
Revisión de 18:54 26 may 2010
Contenido |
1 Enunciado
Se tiene un bloque de hielo de 500 g de hielo sumergido en 500 g de agua, ambos a 0°C. El conjunto está contenido en un recipiente cilíndrico de vidrio, de 16 cm de diámetro y 1 cm de espesor, abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). El recipiente está sumergido en un baño de agua a 20°C.
- Calcule la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1 s.
- Halle la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará en derretirse por completo?
- Calcule la variación de entropía en el sistema, en el ambiente y la variación de entropía total. ¿Es este proceso posible?
Datos: Conductividad térmica del vidrio 1.1 W/m·K; Entalpía específica de fusión: L_f = \Delta h_f = 333.55 kJ/kg
2 Flujo de calor
Podemos obtener la cantidad de calor que entra por segundo a partir de la expresión para la conducción de calor
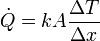
En este caso A es el área lateral del recipiente. Este área es la de la base, más la parte de cara lateral hasta la altura a la que llega el agua. hallamos primero esta altura
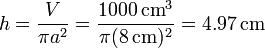
Nótese que no hace falta distinguir entre agua e hielo, ya que por tratarse de la misma sustancia, el principio de Arquímedes nos dice que el volumen desalojado de agua por 0.5 kg de hielo es justamente 0.5 litros.
La superficie de agua en contacto con el vidrio es
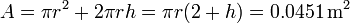
En la expresión del flujo de calor ΔT la diferencia de temperaturas entre las dos caras (20 K) y Δx el espesor del recipiente (0.01 m). Por tanto