Campo producido por una espira poligonal
De Laplace
(→Momento magnético) |
(→Campo en P) |
||
| Línea 69: | Línea 69: | ||
==Espira alabeada== | ==Espira alabeada== | ||
===Campo en P=== | ===Campo en P=== | ||
| - | [[Imagen:espiracubo.png|left]]En el segundo caso tenemos las contribuciones de seis tramos. El punto P se encuentra a la misma distancia <math>a</math> de los seis tramos. | + | [[Imagen:espiracubo.png|left]]En el segundo caso tenemos las contribuciones de seis tramos. El punto <math>P</math> se encuentra a la misma distancia <math>a</math> de los seis tramos. |
| - | + | Para las contribuciones de cada tramo, debemos distinguir entre dos casos. | |
| - | + | Consideremos los dos tramos situados en el plano XY. Para el primero (en el sentido de la corriente) tenemos que | |
| - | <center><math>\ | + | <center><math>\alpha_1=0\,</math>{{qquad}}{{qquad}}<math>\alpha_2=\frac{\pi}{4}</math>{{qquad}}{{qquad}}<math>\mathbf{n}=\mathbf{u}_z</math></center> |
| - | + | con lo que su contribución al campo magnético es | |
| - | <center><math>\mathbf{ | + | <center><math>\mathbf{B}_1=\frac{\mu_0I}{4\pi a}\left(\frac{1}{\sqrt{2}}-0\right)\mathbf{u}_z=\frac{\mu_0I}{4\sqrt{2}\pi a}\mathbf{u}_z</math></center> |
| - | y el campo magnético en P | + | Para el segundo tramo del mismo plano, se cumple |
| + | |||
| + | <center><math>\alpha_1=-\frac{\pi}{4}\,</math>{{qquad}}{{qquad}}<math>\alpha_2=0\,</math>{{qquad}}{{qquad}}<math>\mathbf{n}=\mathbf{u}_z</math></center> | ||
| + | |||
| + | y el campo debido a este segmento en <math>P</math> es | ||
| + | |||
| + | <center><math>\mathbf{B}_2=\frac{\mu_0I}{4\pi a}\left(0-\left(-\frac{1}{\sqrt{2}}\right)\right)\mathbf{u}_z=\frac{\mu_0I}{4\sqrt{2}\pi a}\mathbf{u}_z</math></center> | ||
| + | |||
| + | esto es, la misma que para el primer segmento. | ||
| + | |||
| + | Del mismo modo se opera para el resto de segmentos, donde lo único que cambia en cada caso es la dirección del vector normal, resultando el campo magnético total en <math>P</math> | ||
<center><math>\mathbf{B}=\frac{\mu_0I\sqrt{2}}{4\pi a}(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z)</math></center> | <center><math>\mathbf{B}=\frac{\mu_0I\sqrt{2}}{4\pi a}(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z)</math></center> | ||
Revisión de 12:49 13 may 2010
Contenido |
1 Enunciado
Por las espira de formas irregulares de las figuras circula una corriente I. Halle el valor del campo en el punto P en cada caso.
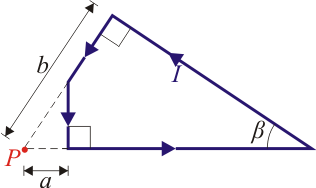
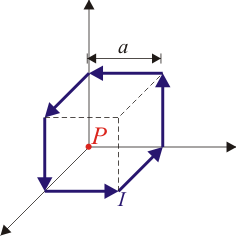
Para cada una de las espiras, hállese su momento magnético y la expresión del campo magnético y del potencial vector en puntos alejados de la espira.
2 Cuadrilátero
2.1 Campo en P
El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. El campo de un segmento puede calcularse por integración directa, resultando la expresión
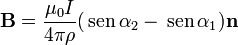
donde α1 y α2 son los ángulos con que se ven los extremos del segmento desde P, ρ es la distancia de P a la recta soporte del segmento y  la normal al plano definido por el segmento y P, orientado según la regla de la mano derecha.
la normal al plano definido por el segmento y P, orientado según la regla de la mano derecha.
Quedan las contribuciones de los otros dos lados.
Para el lado situado a una distancia a tenemos que
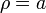
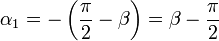
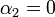
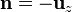
 es el vector perpendicular al plano de la espira, hacia adentro de la pantalla. La contribución de esta lado es
es el vector perpendicular al plano de la espira, hacia adentro de la pantalla. La contribución de esta lado es
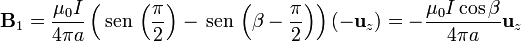
Para el lado situado a una distancia b tenemos que
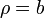
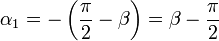
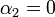
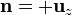
La contribución de esta lado es
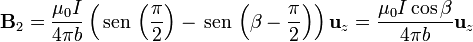
y el campo en P
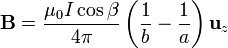
Puesto que a < b, este campo va hacia adentro de la pantalla.
2.2 Momento magnético
El momento magnético de una espira plana es
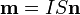
Siendo S el área de la porción de plano limitada por la curva y n la normal a éste (con el sentido asignado por la regla de la mano derecha.
El área de esta figura es la de un triángulo rectángulo menos la de otro triángulo rectángulo semejante
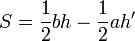
con h y h' las longitudes de los lados 2 y 4. Por trigonomtría
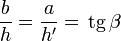
y
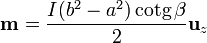
El campo en puntos alejados el potencial vector es el de un dipolo
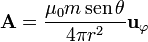
El campo correspondiente es
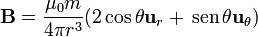
3 Espira alabeada
3.1 Campo en P
En el segundo caso tenemos las contribuciones de seis tramos. El punto P se encuentra a la misma distancia a de los seis tramos.Para las contribuciones de cada tramo, debemos distinguir entre dos casos.
Consideremos los dos tramos situados en el plano XY. Para el primero (en el sentido de la corriente) tenemos que
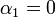
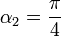
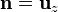
con lo que su contribución al campo magnético es
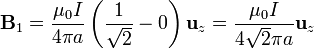
Para el segundo tramo del mismo plano, se cumple
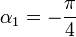
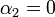
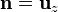
y el campo debido a este segmento en P es
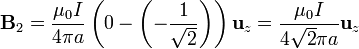
esto es, la misma que para el primer segmento.
Del mismo modo se opera para el resto de segmentos, donde lo único que cambia en cada caso es la dirección del vector normal, resultando el campo magnético total en P
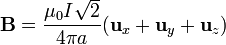
3.2 Momento magnético
El momento magnético de esta espira es
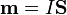
con 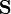 el vector superficie que, para una curva alabeada es un vector cuyas componentes son las áreas de las proyecciones d ela curva sobre los tres planos coordenados. Para esta quebrada, las proyecciones son sendos cuadrados de lado a. Por ello
el vector superficie que, para una curva alabeada es un vector cuyas componentes son las áreas de las proyecciones d ela curva sobre los tres planos coordenados. Para esta quebrada, las proyecciones son sendos cuadrados de lado a. Por ello
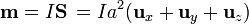
Para el campo en puntos alejados sustituimos en la expresión general
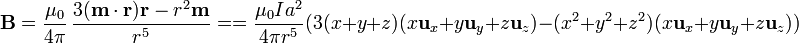
Agrupando por componentes






