Medio polarizado entre dos placas
De Laplace
(→Diferencia de potencial inicial) |
(→Diferencia de potencial inicial) |
||
| Línea 19: | Línea 19: | ||
<center><math>\rho_p = -\nabla\cdot\mathbf{P}_0=0</math></center> | <center><math>\rho_p = -\nabla\cdot\mathbf{P}_0=0</math></center> | ||
| - | Sí existe una densidad de carga de polarización en las superficies del dieléctrico, contiguas a las placas. En la cara superior (aquella a la cual apunta la polarización) | + | Sí existe una densidad de carga de polarización en las superficies del dieléctrico, contiguas a las placas. |
| + | |||
| + | * En la cara superior (aquella a la cual apunta la polarización) | ||
<center><math>\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]=-\mathbf{u}_z\cdot(\mathbf{0}-P_0\mathbf{u}_z)=P_0</math></center> | <center><math>\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]=-\mathbf{u}_z\cdot(\mathbf{0}-P_0\mathbf{u}_z)=P_0</math></center> | ||
| + | |||
| + | * En la cara inferior (desde la cual apunta la polarización) | ||
| + | |||
| + | <center><math>\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]=-\mathbf{u}_z\cdot(P_0\mathbf{u}_z-\mathbf{0})=-P_0</math></center> | ||
| + | |||
| + | Nótese que cuando se calcula la densidad superficial de carga de polarización usando el salto en la polarización, no es necesario tomar la normal exterior. | ||
| + | |||
| + | Tenemos entonces que el sistema equivale a dos superficies cargadas, con densidades <math>\pm P_0</math>. Si despreciamos los efectos de borde, las superficies cargadas se pueden tratar como si fueran infinitamente extensas. En ese caso, tal como se ve en el problema del [[campo debido a dos planos paralelos]], el campo que se produce es | ||
| + | |||
| + | <center><math>\mathbf{E}=-\frac{P_0}{\varepsilon_0}\qquad (0<z<a)</math></center> | ||
| + | |||
| + | en el espacio entre las plcas y nulo en el resto del espacio. | ||
| + | |||
| + | Puesto que este campo es uniforme, la diferencia de potencial es inmediata | ||
| + | |||
| + | <center><math>V_0-V_a = \int_0^a E\,\mathrm{d}z = -\frac{P_0a}{\varepsilon_0}</math></center> | ||
| + | |||
| + | Puesto que el campo va en el sentido opuesto a la polarización, la placa inferior se encuentra a un potencial más bajo que la superior. | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 18:55 8 may 2010
1 Enunciado
Entre dos placas metálicas planas y paralelas, de sección S y separadas una distancia a, se encuentra un dieléctrico que presenta polarización remanente, de forma que en él
siendo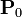 
un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
- Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste?
- Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica?
- Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como
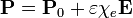
2 Diferencia de potencial inicial
El voltímetro actúa como un circuito abierto, de forma que a todos los efectos es como si las placas siguieran estando desconectadas la una de la otra.
Puesto que las placas están descargadas, la única carga en este sistema es la de polarización, debida al dieléctrico. Por ser su polarización uniforme, no hay densidad volumétrica de carga
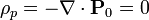
Sí existe una densidad de carga de polarización en las superficies del dieléctrico, contiguas a las placas.
- En la cara superior (aquella a la cual apunta la polarización)
![\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]=-\mathbf{u}_z\cdot(\mathbf{0}-P_0\mathbf{u}_z)=P_0](/wiki/images/math/4/e/a/4eaee2b0d2d15541df8b02cf939b0944.png)
- En la cara inferior (desde la cual apunta la polarización)
![\sigma_p = -\mathbf{n}\cdot[\mathbf{P}]=-\mathbf{u}_z\cdot(P_0\mathbf{u}_z-\mathbf{0})=-P_0](/wiki/images/math/b/2/5/b25482fb62b6cdd9ee798834fff57a12.png)
Nótese que cuando se calcula la densidad superficial de carga de polarización usando el salto en la polarización, no es necesario tomar la normal exterior.
Tenemos entonces que el sistema equivale a dos superficies cargadas, con densidades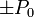 
. Si despreciamos los efectos de borde, las superficies cargadas se pueden tratar como si fueran infinitamente extensas. En ese caso, tal como se ve en el problema del campo debido a dos planos paralelos, el campo que se produce es
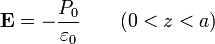
en el espacio entre las plcas y nulo en el resto del espacio.
Puesto que este campo es uniforme, la diferencia de potencial es inmediata
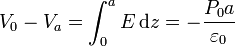
Puesto que el campo va en el sentido opuesto a la polarización, la placa inferior se encuentra a un potencial más bajo que la superior.
