Vector desplazamiento
De Laplace
(Diferencias entre revisiones)
(→Ecuaciones de la electrostática en dieléctricos) |
(→Ecuaciones de la electrostática en dieléctricos) |
||
| Línea 13: | Línea 13: | ||
<center><math>\oint_{\partial\tau} \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_p+Q_l}{\varepsilon_0}</math>{{qquad}}{{qquad}}<math>\oint_\Gamma \mathbf{E}\cdot\mathrm{d}\mathbf{r}=0</math></center> | <center><math>\oint_{\partial\tau} \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_p+Q_l}{\varepsilon_0}</math>{{qquad}}{{qquad}}<math>\oint_\Gamma \mathbf{E}\cdot\mathrm{d}\mathbf{r}=0</math></center> | ||
| + | |||
| + | Cuando tanto las densidades de carga libre como la polarización del medio son cantidades conocidas, estas ecuaciones (junto con las correspondientes condiciones de salto y de contorno) permiten determinar completamente el campo eléctrico. | ||
==Definición del vector desplazamiento== | ==Definición del vector desplazamiento== | ||
Revisión de 20:03 1 mar 2010
Contenido |
1 Ecuaciones de la electrostática en dieléctricos
Cuando se tienen en cuenta las densidades de carga de polarización las ecuaciones de la electrostática se escriben
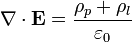
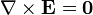
siendo
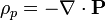
la densidad volumétrica de carga de polarización y ρl la densidad volumétrica de carga libre, esto es, aquella que no está asociada a la polarización del material.
En forma integral estas ecuaciones se escriben
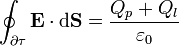
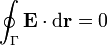
Cuando tanto las densidades de carga libre como la polarización del medio son cantidades conocidas, estas ecuaciones (junto con las correspondientes condiciones de salto y de contorno) permiten determinar completamente el campo eléctrico.





