Propulsión solar
De Laplace
(→Colisión perfectamente elástica) |
(→Colisión perfectamente elástica) |
||
| Línea 86: | Línea 86: | ||
Esto conduce a las ecuaciones | Esto conduce a las ecuaciones | ||
| - | <center><math>p_1+p_2=p'_1+p'_2\,</math>{{qquad}}{{qquad}} <math>E_1+E_2 = E'_1+E'_2</math>{{qquad}}{{qquad}} <math>{E'_1}^2-{p'_1}^2=E_1^2-p_1^2=m_1^2\,</math>{{qquad}}{{qquad}}<math>{E'_1}^2-{p'_1}^2=E_1^2-p_1^2=m_1^2\,</math></center> | + | <center><math>p_1+p_2=p'_1+p'_2\,</math>{{qquad}}{{qquad}} <math>E_1+E_2 = E'_1+E'_2\,</math>{{qquad}}{{qquad}} <math>{E'_1}^2-{p'_1}^2=E_1^2-p_1^2=m_1^2\,</math>{{qquad}}{{qquad}}<math>{E'_1}^2-{p'_1}^2=E_1^2-p_1^2=m_1^2\,</math></center> |
| + | |||
| + | En términos de las celeridades | ||
| + | |||
| + | <center><math>m_1\sinh\phi_1+m_2\sinh\phi_2=m_1\sinh\phi'_1+m_2\sinh\phi'_2</math>{{qquad}}{{qquad}}<math>m_1\cosh\phi_1+m_2\cosh\phi_2=m_1\cosh\phi'_1+m_2\cosh\phi'_2</math></center> | ||
====Colisión completamente inelástica==== | ====Colisión completamente inelástica==== | ||
Revisión de 10:36 21 feb 2010
Contenido |
1 Introducción
2 Fundamentos
2.1 Partículas y cuadrivectores
La cantidad de movimiento energía de una partícula puede describirse por el cuadrivector
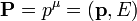
donde la parte espacial es la cantidad de movimiento ordinaria, y la parte temporal es la energía de la partícula. El módulo de este cuadrivector es el cuadrado de la masa en reposo de la partícula.
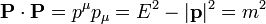
En este problema, en que todo ocurre en una sola dimensión, la parte espacial se reduce a una sola componente

por lo que podemos prescindir de la segunda y la tercera y escribir simplemente
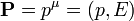
con el módulo
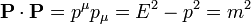
2.2 Fotones
Los fotones individuales se pueden considerar como partículas de masa nula, por lo que el cuadrivector correspondiente será de la forma
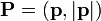
que, en el caso unidimensional se reduce a
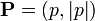
De acuerdo con las relaciones de Einstein-de Broglie, la cantidad de movimiento y la energía de un fotón son proporcionales a su número de onda y a su frecuencia, respectivamente. En términos de los cuadrivectores


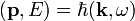
cumpliéndose la relación
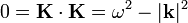


En el caso unidimensional, el cuadrivector número de onda será
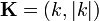
2.3 Transformaciones de Lorentz
Una transformación de Lorentz en la dirección del eje X es de la forma

con
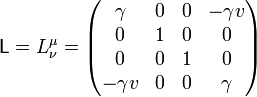
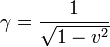
Esta matriz se puede escribir de forma alternativa introduciendo la celeridad
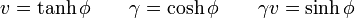

Si consideramos un problema unidmensional, la matriz se reduce a una 2×2:
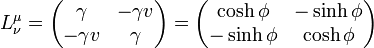
La transformación de Lorentz inversa corresponde a cambiar v por − v (o  por
por 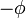 ).
).
2.4 Efecto Doppler
Si aplicamos la transformación de Lorentz a un fotón, obtenemos que el cuadrivector número de onda se transforma en
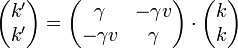
esto es
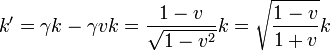
o, en términos de la celeridad
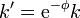
El número de onda, y por tanto la frecuencia, se ven reducidos al observar el mismo fotón en un sistema que se aleja con velocidad v respecto al primero. Este es el corrimiento al rojo. Por supuesto, si el fotón va en sentido contrario al nuevo observador, lo que se aprecia es un aumento de la frecuencia, un corrimiento hacia el violeta.
3 Colisiones relativistas
3.1 Entre dos partículas
3.1.1 Colisión perfectamente elástica
En una colisión perfectamente elástica, las partículas salen despedidas conservando sus masas individuales, de forma que tenemos
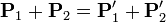
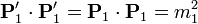
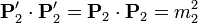
Esto conduce a las ecuaciones
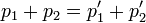
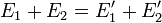
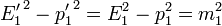
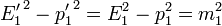
En términos de las celeridades





