Propulsión solar

De Laplace

Contenido

1 Introducción
2 Fundamentos
3 Colisión con un fotón
- 3.1 Absorción de un fotón
- 3.2 Reflexión de un fotón
4 Barco de vela solar
5 Nave radiante
6 Presión de radiación

1 Introducción

2 Fundamentos

2.1 Partículas y cuadrivectores

La cantidad de movimiento energía de una partícula puede describirse por el cuadrivector

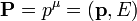
$\mathbf{P}=p^\mu=(\mathbf{p},E)$

donde la parte espacial es la cantidad de movimiento ordinaria, y la parte temporal es la energía de la partícula.

Este vector es proporcional cuadrivector velocidad

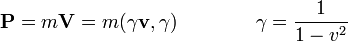
$\mathbf{P}=m\mathbf{V}=m(\gamma\mathbf{v},\gamma)\qquad\qquad\gamma = \frac{1}{1-v^2}$

dado que la velocidad es un cuadrivector de módulo unidad, el módulo del cuadrivector cantidad de movimiento es el cuadrado de la masa en reposo de la partícula.

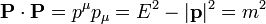
$\mathbf{P}\cdot\mathbf{P}=p^\mu p_\mu = E^2 - |\mathbf{p}|^2 = m^2$

En este problema, en que todo ocurre en una sola dimensión, la parte espacial se reduce a una sola componente

$\mathbf{P}=p^\mu = (p,0,0,E)\,$

por lo que podemos prescindir de la segunda y la tercera y escribir simplemente

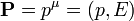
$\mathbf{P}=p^\mu = (p,E)\,$

con el módulo

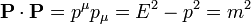
$\mathbf{P}\cdot\mathbf{P}=p^\mu p_\mu = E^2-p^2 = m^2\,$

La cuadrivelocidad se reduce a

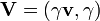
$\mathbf{V}=(\gamma\mathbf{v},\gamma)\,$

Introduciendo la celeridad $\phi\,$

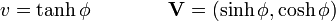
$v=\tanh\phi\qquad\qquad \mathbf{V}=(\sinh\phi,\cosh\phi)$

2.2 Fotones

Los fotones individuales se pueden considerar como partículas de masa nula, por lo que el cuadrivector correspondiente será de la forma

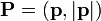
$\mathbf{P}= (\mathbf{p},|\mathbf{p}|)\,$

que, en el caso unidimensional se reduce a

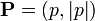
$\mathbf{P} = (p,|p|)\,$

De acuerdo con las relaciones de Einstein-de Broglie, la cantidad de movimiento y la energía de un fotón son proporcionales a su número de onda y a su frecuencia, respectivamente. En términos de los cuadrivectores

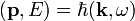
$\mathbf{P}= \hbar \mathbf{K}$ $\Rightarrow$ $(\mathbf{p},E) = \hbar(\mathbf{k},\omega)$

cumpliéndose la relación

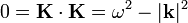
$0 = \mathbf{K}\cdot\mathbf{K} = \omega^2 - |\mathbf{k}|^2\,$ $\Rightarrow$ $\omega = |\mathbf{k}|\,$

En el caso unidimensional, el cuadrivector número de onda será

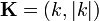
$\mathbf{K} = (k,|k|)\,$

2.3 Transformaciones de Lorentz

Una transformación de Lorentz en la dirección del eje X es de la forma

$\mathbf{P}'=\mathsf{L}\cdot\mathbf{P}\qquad\qquad p'^\mu = L^\mu_\nu p^\nu$

con

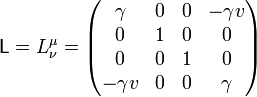
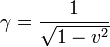
$\mathsf{L}=L^\mu_\nu = \begin{pmatrix}\gamma & 0 & 0 & -\gamma v\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\gamma v & 0 & 0 & \gamma\end{pmatrix}$ $\gamma=\frac{1}{\sqrt{1-v^2}}$

Esta matriz se puede escribir de forma alternativa introduciendo la celeridad del movimiento relativo

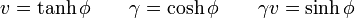
$v = \tanh\phi\qquad \gamma = \cosh\phi\qquad\gamma v = \sinh\phi$ $L^\mu_\nu = \begin{pmatrix}\cosh\phi & 0 & 0 & -\sinh\phi\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\sinh\phi & 0 & 0 & \cosh\phi\end{pmatrix}$

Si consideramos un problema unidmensional, la matriz se reduce a una 2×2:

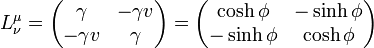
$L^\mu_\nu = \begin{pmatrix}\gamma & -\gamma v\\ -\gamma v & \gamma\end{pmatrix}=\begin{pmatrix}\cosh\phi & -\sinh\phi\\ -\sinh\phi & \cosh\phi\end{pmatrix}$

La transformación de Lorentz inversa corresponde a cambiar $v$ por $- v$ (o $\phi\,$ por $-\phi\,$ ).

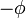2.4 Efecto Doppler

Si aplicamos la transformación de Lorentz a un fotón, obtenemos que el cuadrivector número de onda se transforma en

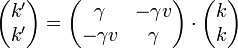
$\begin{pmatrix}k' \\ k'\end{pmatrix} = \begin{pmatrix} \gamma & -\gamma v\\ -\gamma v & \gamma \end{pmatrix}\cdot\begin{pmatrix}k \\ k \end{pmatrix}$

esto es

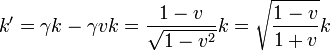
$k' = \gamma k -\gamma v k = \frac{1-v}{\sqrt{1-v^2}}k = \sqrt{\frac{1-v}{1+v}}k$

o, en términos de la celeridad

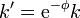
$k' = \mathrm{e}^{-\phi}k\,$

El número de onda, y por tanto la frecuencia, se ven reducidos al observar el mismo fotón en un sistema que se aleja con velocidad v respecto al primero. Este es el corrimiento al rojo. Por supuesto, si el fotón va en sentido contrario al nuevo observador, lo que se aprecia es un aumento de la frecuencia, un corrimiento hacia el violeta.

3 Colisión con un fotón

En una colisión relativista siempre se conserva la cantidad de movimiento-energía, por lo que la ecuación básica que determina el resultado de una colisión es

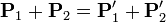
$\mathbf{P}_1+\mathbf{P}_2=\mathbf{P}'_1+\mathbf{P}'_2\,$

La colisión con un fotón puede tratarse como una colisión entre dos partículas, una de ellas de masa nula.

3.1 Absorción de un fotón

En una colisión inelástica el blanco se comporta como un cuerpo negro y absorbe un fotón, resultando una nueva partícula de mayor masa.

El balance es

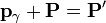
$\mathbf{p}_\gamma+\mathbf{P}=\mathbf{P}'$ $\Rightarrow$ $p +P=P'\,$ $p+E=E'\,$

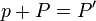
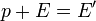
La nueva masa de la partícula cumple

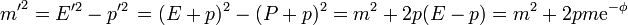
${m'}^2 = E'^2-p'^2\,=(E+p)^2-(P+p)^2 = m^2 + 2p(E-p)=m^2+2p m \mathrm{e}^{-\phi}$

Si al energía del fotón es muy pequeña comparada con la masa de la partícula, esto vale, aproximadamente

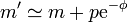
$m'\simeq m + p \mathrm{e}^{-\phi}$

El aumento de la masa es menor cuanto más rápido se mueva.

La nueva velocidad de la partícula resultante es

$v'=\frac{P+p}{E+p}$

Si queremos el incremento de velocidad

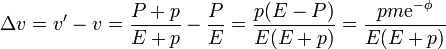
$\Delta v = v'-v = \frac{P+p}{E+p}-\frac{P}{E}=\frac{p(E-P)}{E(E+p)} = \frac{p m \mathrm{e}^{-\phi}}{E(E+p)}$

Si consideramos de nuevo pequeña la energía del fotón comparada con la de la partícula

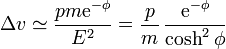
$\Delta v \simeq \frac{p m \mathrm{e}^{-\phi}}{E^2} =\frac{p}{m}\,\frac{\mathrm{e}^{-\phi}}{\cosh^2\phi}$

3.2 Reflexión de un fotón

En una colisión elástica, se absorbe un fótón y se emite otro en el sentido contrario, manteniéndose la masa del blanco, por lo que tenemos las ecuaciones

$\mathbf{P}+\mathbf{p}=\mathbf{P}'+\mathbf{p}'\qquad\qquad\mathbf{P}'\cdot\mathbf{P}'=\mathbf{P}\cdot\mathbf{P}=m^2$

Despejando y hallando el módulo

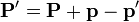
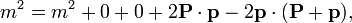
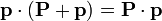
$\mathbf{P}'=\mathbf{P}+\mathbf{p}-\mathbf{p}'\,$ $\Rightarrow$ $m^2 = m^2 + 0 + 0 +2\mathbf{P}\cdot\mathbf{p}-2\mathbf{p}\cdot(\mathbf{P}+\mathbf{p})º,$ $\Rightarrow$ $\mathbf{p}\cdot(\mathbf{P}+\mathbf{p})=\mathbf{P}\cdot\mathbf{p}$

Escribiendo los momentos de los fotones incidente y reflejado como

$\mathbf{p}=(p,p)\qquad\qquad\mathbf{p}'=(-p',p)$

obtenemos

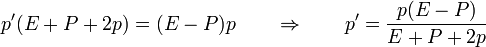
$p'(E+P+2p)=(E-P)p\qquad\Rightarrow\qquad p'=\frac{p(E-P)}{E+P+2p}$

De aquí resulta la nueva cantidad de movimiento para el blanco, y el incremento en cantidad de movimiento

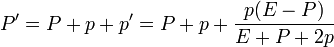
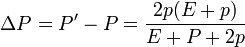
$P'=P+p+p'=P+p + \frac{p(E-P)}{E+P+2p}$ $\Delta P = P'-P=\frac{2p(E+p)}{E+P+2p}$

La nueva energía y su incremento

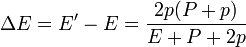
$E'=E+p-p'=E+p - \frac{p(E-P)}{E+P+2p}$ $\Delta E = E'-E=\frac{2p(P+p)}{E+P+2p}$

La nueva velocidad y su incremento

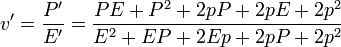
$v'=\frac{P'}{E'} = \frac{PE+P^2+2pP+2pE+2p^2}{E^2+EP+2Ep+2pP+2p^2}$ $\Delta v = \frac{2p(E-P)(E+P-p)}{E(E^2+EP+2Ep+2pP+2p^2)}$

Si suponemos que la cantidad de movimiento del fotón es muy pequeña comparada con la masa del blanco, obtenemos

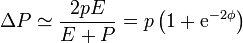
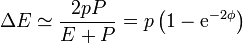
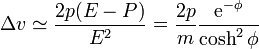
$\Delta P\simeq \frac{2pE}{E+P}=p\left(1+\mathrm{e}^{-2\phi}\right)$ $\Delta E \simeq \frac{2pP}{E+P}=p\left(1-\mathrm{e}^{-2\phi}\right)$ $\Delta v\simeq \frac{2p(E-P)}{E^2}=\frac{2p}{m}\frac{\mathrm{e}^{-\phi}}{\cosh^2\phi}$

4 Barco de vela solar

4.1 Descripción del problema

Tenemos una nave de masa en reposo inicial $m 0$ sobre la que va impactando un rayo láser monocromático. Se trata de averiguar cómo aumenta la velocidad de la nave.

El cañón láser emite con una intensidad $I 0$ , de forma que de él salen $N$ fotones en la unidad de tiempo, cada uno con momento $p$ (o número de onda 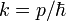$k=p/\hbar$ ).

En lugar de suponer que salen los N fotones de una vez, o de forma continua, podemos admitir que sale espaciados con un intervalo $τ = 1 / N$ , de forma que

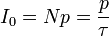
$I_0=Np = \frac{p}{\tau}$

Los fotones van impactando sucesivamente en la nave, yendo cada uno una distancia $τ$ tras el anterior. Entonces, si la nave tras la colisión con el n-simo fotón tiene una velocidad $v n$ , la siguiente colisión se producirá cuando el fotón que viene detrás alcance a la nave, lo cual ocurrirá un $Δ t n$ más tarde con la condición

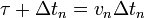
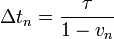
$\tau + \Delta t_n = v_n\Delta t_n\,$ $\Rightarrow$ $\Delta t_n = \frac{\tau}{1-v_n}$

Después de esa nueva colisión, la velocidad pasa a ser $v n + 1$ , o equivalentemente

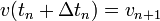
$v(t_n+\Delta t_n) = v_{n+1}\,$

Desarrollando aquí, si $τ$ es muy corto

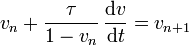
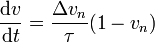
$v_n + \frac{\tau}{1-v_n}\,\frac{\mathrm{d}v}{\mathrm{d}t} = v_{n+1}$ $\Rightarrow$ $\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\Delta v_n}{\tau}(1-v_n)$

y de manera similar obtenemos ecuaciones para la cantidad de movimiento y la energía

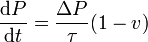
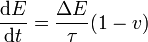
$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{\Delta P}{\tau}(1-v)$ $\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{\Delta E}{\tau}(1-v)$

El resultado concreto depende de si el fotón incidente es reflejado o absorbido.

4.2 Vela absorbente

En el caso de la vela absorbente (cuerpo negro), la cantidad de movimiento y la energía se incrementan en $p$ en cada colisión, por lo que

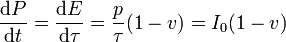
$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{\mathrm{d}E}{\mathrm{d}\tau}=\frac{p}{\tau}(1-v) = I_0(1-v)$

De la primera igualdad

$E=P+m_0\,$

con $m 0$ la masa inicial de la nave. Despejando P y sustituyendo en la ecuación de la energía

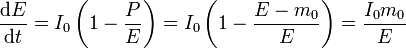
$\frac{\mathrm{d}E}{\mathrm{d}t}=I_0\left(1-\frac{P}{E}\right)=I_0\left(1-\frac{E-m_0}{E}\right)=\frac{I_0m_0}{E}$

y la integración de esta ecuación es inmediata. Si suponemos que la nave parte del reposo

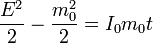
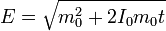
$\frac{E^2}{2}-\frac{m_0^2}{2}=I_0m_0 t$ $\Rightarrow$ $E=\sqrt{m_0^2+2I_0m_0 t}$

La cantidad de movimiento y la velocidad son

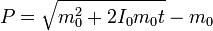
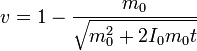
$P = \sqrt{m_0^2+2I_0m_0 t}-m_0\,$ $v=1-\frac{m_0}{\sqrt{m_0^2+2I_0m_0 t}}$

Integrando obtenemos la posición como función del tiempo

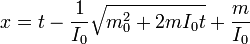
$x = t -\frac{1}{I_0} \sqrt{m_0^2+2m I_0t}+\frac{m}{I_0}$

De aquí resulta una masa como función del tiempo

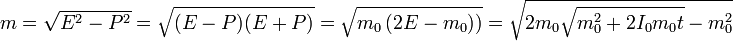
$m= \sqrt{E^2-P^2}= \sqrt{(E-P)(E+P)}=\sqrt{m_0\left(2E-m_0)\right)}=\sqrt{2m_0\sqrt{m_0^2+2I_0m_0 t}-m_0^2}$

La raíz interior se relaciona directamente con la velocidad

$\sqrt{m_0^2+2I_0m_0 t} = \frac{m_0}{1-v}$

por lo que nos queda

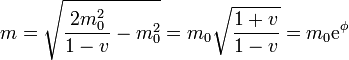
$m = \sqrt{\frac{2m_0^2}{1-v}-m_0^2}=m_0\sqrt{\frac{1+v}{1-v}}=m_0\mathrm{e}^\phi$

Sin pasar por la dependencia temporal podíamos haber observado que

$P=m\sinh\phi\qquad\qquad E = m\cosh\phi\,$

y puesto que su diferencia es $m 0$

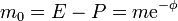
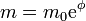
$m_0= E-P = m \mathrm{e}^{-\phi}\,$ $\Rightarrow$ $m = m_0\mathrm{e}^\phi\,$

que es mucho más simple.

4.3 Vela reflectante

En el caso de una vela reflectante, sustituyendo los incrementos en la cantidad de movimiento y la energía queda

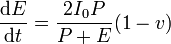
$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{2I_0E}{P+E}(1-v)$ $\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{2I_0P}{P+E}(1-v)$

En este caso lo que se conserva es la masa en reposo de la nave

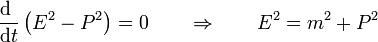
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(E^2-P^2\right)=0\qquad\Rightarrow\qquad E^2 = m^2+P^2$

De la ecuación para la cantidad de movimiento tenemos (usando que $v = P / E$ )

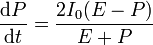
$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{2I_0(E-P)}{E+P}$

En función de la celeridad

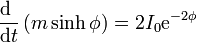
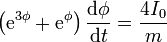
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(m\sinh\phi\right)= 2I_0\mathrm{e}^{-2\phi}$ $\Rightarrow$ $\left(\mathrm{e}^{3\phi}+\mathrm{e}^{\phi}\right)\frac{\mathrm{d}\phi}{\mathrm{d}t}=\frac{4I_0}{m}$

Integrando

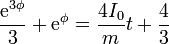
$\frac{\mathrm{e}^{3\phi}}{3}+\mathrm{e}^\phi = \frac{4I_0}{m}t+\frac{4}{3}$

Esto nos da una ecuación cúbica en 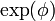$\exp(\phi)\,$ cuya solución permite hallar $v$ , $P$ y $E$ .

Para hallar la posición como función de la celeridad aplicamos que

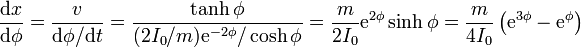
$\frac{\mathrm{d}x}{\mathrm{d}\phi}=\frac{v}{\mathrm{d}\phi/\mathrm{d}t}=\frac{\tanh\phi}{(2I_0/m)\mathrm{e}^{-2\phi}/\cosh\phi}=\frac{m}{2I_0}\mathrm{e}^{2\phi}\sinh\phi = \frac{m}{4I_0}\left(\mathrm{e}^{3\phi}-\mathrm{e}^\phi\right)$

Integrando

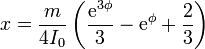
$x = \frac{m}{4I_0}\left(\frac{\mathrm{e}^{3\phi}}{3}-\mathrm{e}^\phi+\frac{2}{3}\right)$

Esta ecuación y las anteriores nos permiten trazar la curvas paramétricas 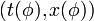$(t(\phi),x(\phi))\,$ y similares

5 Nave radiante

Supongamos que la nave emite radiación (por ejemplo, por estar a una cierta temperatura) de manera isótropa en su propio sistema de referencia, de manera que su masa permanece constante.

Una nave de esta clase, tras absorber un fotón e incrementar su cuadrivector cantidad de movimiento como en el caso absorbente

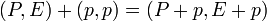
$(P,E) + (p,p) = (P+p,E+p)\,$

experimenta una reducción en su masa de forma que ésta sigue siendo $m 0$ , por lo que tras la reemisión el nuevo cuadrivector es

$(P+p,E+p)\to \frac{m_0}{\sqrt{(E+p)^2-(P+p)^2}}(P+p,E+p)=\frac{m_0}{\sqrt{m_0^2+2(E-P)p}}(P+p,E+p)$

En el proceso combinado de absorción-radiación, el incremento en la cantidad de movimiento y en la energía es entonces

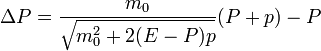
$\Delta P = \frac{m_0}{\sqrt{m_0^2+2(E-P)p}}(P+p)-P$ $\Delta E = \frac{m_0}{\sqrt{m_0^2+2(E-P)p}}(E+p)-E$

Lo que nos lleva a las ecuaciones diferenciales para la cantidad de movimiento

$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{\Delta P}{\tau}(1-v)=I_0(1-v)\left(\frac{m_0(P+p)}{p\sqrt{m_0^2+2(E-P)p}}-\frac{P}{p}\right)$

y la energía

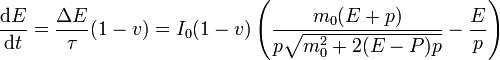
$\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{\Delta E}{\tau}(1-v)=I_0(1-v)\left(\frac{m_0(E+p)}{p\sqrt{m_0^2+2(E-P)p}}-\frac{E}{p}\right)$

Desarrollando y reteniendo hasta primer orden en $p$ ,

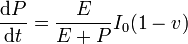
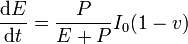
$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{E}{E+P}I_0(1-v)$ $\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{P}{E+P}I_0(1-v)$

Estas ecuaciones son exactamente las mismas que para el caso de la vela reflectante, pero con $I 0$ en lugar de $2 I 0$ , por lo que la solución es la misma que allí, pero con la mitad de intensidad.

6 Presión de radiación

En el caso absorbente, visto desde el laboratorio, la nave se acelera exclusivamente por la presión que el haz de fotones ejerce sobre ella.

Propulsión solar

De Laplace

Contenido

1 Introducción

2 Fundamentos

2.1 Partículas y cuadrivectores

2.2 Fotones

2.3 Transformaciones de Lorentz

2.4 Efecto Doppler

3 Colisión con un fotón

3.1 Absorción de un fotón

3.2 Reflexión de un fotón

4 Barco de vela solar

4.1 Descripción del problema

4.2 Vela absorbente

4.3 Vela reflectante

5 Nave radiante

6 Presión de radiación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES