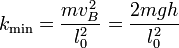Partícula que impacta con un muelle
De Laplace
(Nueva página: ==Enunciado== Una masa <math>m</math> se encuentra al borde de una pendiente. Después de la pendiente se extiende una llanura, al final de la cual hay un muelle relajado de constante...) |
|||
| Línea 9: | Línea 9: | ||
==Velocidad de impacto== | ==Velocidad de impacto== | ||
| + | Cuando la partícula desciende la rampa, se ve sometida a dos fuerzas: su peso y la reacción de la superficie. Esta última es siempre perpendicular a la propia superficie y por tanto al desplazamiento de la partícula, esto es, no realiza trabajo alguno sobre ella. Por tanto, se puede aplicar el teorema de conservación de la energía mecánica usando exclusivamente la energía cinética y la energía potencial gravitatoria. | ||
| + | |||
| + | <center><math>\frac{1}{2}mv_0^2 + mgz_0 = \frac{1}{2}mv_A^2 + mg z_A</math></center> | ||
| + | |||
| + | La velocidad inicial y la altura final son las dos nulas, mientras que la altura inicial es <math>h</math> por lo que | ||
| + | |||
| + | <center><math>mgh = \frac{1}{2}mv_A^2\qquad\Rightarrow\qquad v_A=\sqrt{2gh}</math></center> | ||
| + | |||
| + | Entre el punto A y el punto B la partícula no se ve sometida a fuerza alguna, por lo que su movimiento es uniforme. La velocidad en B, cuando impacta con el muelle, es la misma que en A | ||
| + | |||
| + | <center><math>v_B = v_A =\sqrt{2gh}</math></center> | ||
| + | |||
==Constante mínima== | ==Constante mínima== | ||
| + | Una vez que impacta con el muelle, éste se comprime y la partícula se frena. Si el muelle es muy blando (<math>k</math> pequeña), el frenado es demasiado suave y la partícula llega a impactar con la pared. Si es muy rígido (<math>k</math> grande), la partícula rebota sin apenas comprimir el muelle. | ||
| + | |||
| + | El valor mínimo de <math>k</math> lo da el que la elongación máxima del muelle (a la que se llega con velocidad nula), coincida con la longitud inicial del muelle, <math>l_0</math>. Aplicando de nuevo la ley de conservación de la energía: | ||
| + | |||
| + | <center><math>\frac{1}{2}mv_B^2=\frac{1}{2}k_\mathrm{min}l_0^2</math>{{tose}}<math>k_\mathrm{min}=\frac{mv_B^2}{l_0^2}=\frac{2mgh}{l_0^2}</math></center> | ||
| + | |||
==Constante con rozamiento== | ==Constante con rozamiento== | ||
==Altura máxima== | ==Altura máxima== | ||
==Valores numéricos== | ==Valores numéricos== | ||
[[Categoría:Problemas de introducción a la dinámica]] | [[Categoría:Problemas de introducción a la dinámica]] | ||
Revisión de 11:24 19 feb 2010
Contenido |
1 Enunciado
Una masa m se encuentra al borde de una pendiente. Después de la pendiente se extiende una llanura, al final de la cual hay un muelle relajado de constante elástica k y longitud natural l0. La masa se encuentra a una altura h relativa al muelle. Suponemos que no existe fuerza de rozamiento entre la masa y la superficie.
- Determine la velocidad con la que la masa impacta en el muelle (punto B).
- ¿Cuál es el valor mínimo de la constante elástica del muelle, kmin, para que este pueda evitar que la masa toque la pared?
- Suponga ahora que entre los puntos A y B hay una región de longitud d en la que existe rozamiento entre la masa y el suelo. Si el coeficiente de rozamiento es μ, ¿cu´al es el nuevo valor mínimo de k en el apartado anterior?
- Supongamos que k > kmin. En la situación de rozamiento del apartado anterior, calcule la velocidad con la que la partícula vuelve al punto A y la altura a la que sube por la pendiente.
- Calcule numéricamente las magnitudes pedidas si
, 
, 
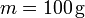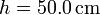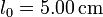, μ = 0.200, 
, 
.
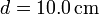2 Velocidad de impacto
Cuando la partícula desciende la rampa, se ve sometida a dos fuerzas: su peso y la reacción de la superficie. Esta última es siempre perpendicular a la propia superficie y por tanto al desplazamiento de la partícula, esto es, no realiza trabajo alguno sobre ella. Por tanto, se puede aplicar el teorema de conservación de la energía mecánica usando exclusivamente la energía cinética y la energía potencial gravitatoria.
La velocidad inicial y la altura final son las dos nulas, mientras que la altura inicial es h por lo que
Entre el punto A y el punto B la partícula no se ve sometida a fuerza alguna, por lo que su movimiento es uniforme. La velocidad en B, cuando impacta con el muelle, es la misma que en A
3 Constante mínima
Una vez que impacta con el muelle, éste se comprime y la partícula se frena. Si el muelle es muy blando (k pequeña), el frenado es demasiado suave y la partícula llega a impactar con la pared. Si es muy rígido (k grande), la partícula rebota sin apenas comprimir el muelle.
El valor mínimo de k lo da el que la elongación máxima del muelle (a la que se llega con velocidad nula), coincida con la longitud inicial del muelle, l0. Aplicando de nuevo la ley de conservación de la energía:
