Densidades de carga de polarización
De Laplace
(→Carga neta) |
(→Momento dipolar) |
||
| Línea 32: | Línea 32: | ||
<center><math>\mathbf{p}= \int_\tau \rho_p\,\mathbf{r}\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathbf{r}\,\mathrm{d}S \equiv\int_\tau\mathbf{P}\,\mathrm{d}\tau</math></center> | <center><math>\mathbf{p}= \int_\tau \rho_p\,\mathbf{r}\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,\mathbf{r}\,\mathrm{d}S \equiv\int_\tau\mathbf{P}\,\mathrm{d}\tau</math></center> | ||
| - | De nuevo este resultado es elemental: si la polarización es la densidad de momento dipolar, su integral nos dará el momento dipolar total | + | De nuevo este resultado es elemental: si la polarización es la densidad de momento dipolar, su integral nos dará el momento dipolar total. |
| + | |||
| + | La demostración es similar a la anterior pero, al tratarse de vectores, es un poco más sofisticada. Consideraremos, en lugar de todo el vector de una vez, solo una de sus componentes, la <math>x</math>, por ejemplo, | ||
| + | |||
| + | <center><math>p_x = \int_\tau\rho_p\,x\,\mathrm{d}\tau+\oint_{\partial\tau}\sigma_p\,x\,\mathrm{d}S</math></center> | ||
| + | |||
| + | Tenemos, por un lado | ||
==Ecxuaciones de la electrostática en dieléctricos== | ==Ecxuaciones de la electrostática en dieléctricos== | ||
[[Categoría:Comportamiento dieléctrico de la materia]] | [[Categoría:Comportamiento dieléctrico de la materia]] | ||
Revisión de 18:19 30 ene 2010
Contenido |
1 Introducción
2 Potencial debido a una polarización
3 Densidades de carga de polarización
3.1 Volumétrica
3.2 Superficial
4 Densidad de carga libre
5 Carga y momento de ρp y σp
Como a toda densidad de carga, a la de polarización se le puede calcular sus momentos multipolares, con el fin de aproximar el potencial que produce una distribución de dipolos en puntos alejados de ella.
5.1 Carga neta
La carga neta (momento monopolar) de una distribución de carga de polarización es siempre nula
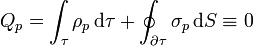
Este resultado es una consecuencia de que la distribución de carga de polarización es equivalente a un conjunto de dipolos. Puesto que cada dipolo es eléctricamente neutro, la carga total del sistema es nula.
Podemos demostrar este resultado a partir de las definiciones de ρp y σp, por aplicación del teorema de Gauss. Por un lado tenemos que
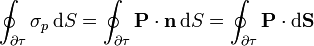
y por otro
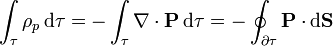
Sumando los dos términos
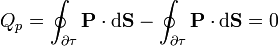
5.2 Momento dipolar
El momento dipolar de la distribución de cargas de polarización equivale a la integral de la polarización
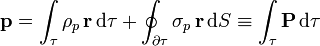
De nuevo este resultado es elemental: si la polarización es la densidad de momento dipolar, su integral nos dará el momento dipolar total.
La demostración es similar a la anterior pero, al tratarse de vectores, es un poco más sofisticada. Consideraremos, en lugar de todo el vector de una vez, solo una de sus componentes, la x, por ejemplo,
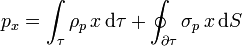
Tenemos, por un lado





