Partícula elíptica en campo eléctrico oblicuo
De Laplace
(Diferencias entre revisiones)
(→Planteamiento) |
(→Coordenadas elípticas) |
||
| Línea 15: | Línea 15: | ||
==Coordenadas elípticas== | ==Coordenadas elípticas== | ||
| + | Para resolver el problema eléctrico empleamos las coordenadas elípticas definidas por | ||
| + | |||
| + | <center><math>x = c \cosh\zeta\cos\eta\,</math>{{qquad}}{{qquad}}<math>y = c \sinh\zeta\sin\eta\,</math></center> | ||
| + | |||
| + | con | ||
| + | |||
| + | <center><math>c = \sqrt{a^2-b^2}</math></center> | ||
| + | |||
| + | En estas coordenadas la superficie de la elipse viene definida por | ||
| + | |||
| + | <center><math>\zeta=\zeta_0=\arctanh\left(\frac{b}{a}\right)</math></center> | ||
| + | |||
==Solución para el potencial== | ==Solución para el potencial== | ||
==Momento dipolar== | ==Momento dipolar== | ||
==Torque== | ==Torque== | ||
Revisión de 18:44 12 ene 2010
Contenido |
1 Planteamiento
Tenemos una elipse de semiejes a y b (a > b) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo α con el semieje mayor.
El problema del potencial se convierte en la solución de la ecuación de Laplace

con la condición de Neumann en la superficie de la partícula

y con el comportamiento asintótico
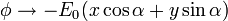
2 Coordenadas elípticas
Para resolver el problema eléctrico empleamos las coordenadas elípticas definidas por
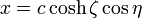
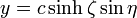
con
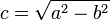
En estas coordenadas la superficie de la elipse viene definida por





