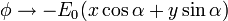Partícula elíptica en campo eléctrico oblicuo
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Planteamiento== ==Coordenadas elípticas== ==Solución para el potencial== ==Momento dipolar== ==Torque==) |
(→Planteamiento) |
||
| Línea 1: | Línea 1: | ||
==Planteamiento== | ==Planteamiento== | ||
| + | Tenemos una elipse de semiejes <math>a</math> y <math>b</math> (<math>a>b</math>) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo <math>\alpha</math> con el semieje mayor. | ||
| + | |||
| + | El problema del potencial se convierte en la solución de la ecuación de Laplace | ||
| + | |||
| + | <math>\nabla^2\phi = 0</math>ççcon la condición de Neumann en la superficie de la partícula | ||
| + | |||
| + | <center><math>\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)</math></center> | ||
| + | |||
| + | y con el comportamiento asintótico | ||
| + | |||
| + | <center><math>\phi\to -E_0(x\cos\alpha+y\sin\alpha)</math></center> | ||
| + | |||
==Coordenadas elípticas== | ==Coordenadas elípticas== | ||
==Solución para el potencial== | ==Solución para el potencial== | ||
==Momento dipolar== | ==Momento dipolar== | ||
==Torque== | ==Torque== | ||
Revisión de 18:30 12 ene 2010
Contenido |
1 Planteamiento
Tenemos una elipse de semiejes a y b (a > b) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo α con el semieje mayor.
El problema del potencial se convierte en la solución de la ecuación de Laplace
ççcon la condición de Neumann en la superficie de la partícula
y con el comportamiento asintótico
