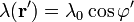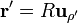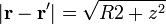Campo de un anillo no uniforme
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== En el plano <math>XY</math> se encuentra una distribución de carga lineal, formando un anillo, de radio <math>R</math> y con una distribución de carga no uniforme dada...) |
(→Potencial en el eje) |
||
| Línea 9: | Línea 9: | ||
==Potencial en el eje== | ==Potencial en el eje== | ||
| + | El potencial en el eje del anillo puede hallarse por integración directa, según la expresión | ||
| + | |||
| + | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}</math></center> | ||
| + | |||
| + | Tenemos que | ||
| + | <center> | ||
| + | <math>\lambda(\mathbf{r}')=\lambda_0\cos\varphi'</math>{{qquad}}{{qquad}}<math>\mathbf{r}=z\mathbf{u}_z\,</math>{{qquad}}{{qquad}}<math>\mathbf{r}'=R\mathbf{u}_{\rho'}\,</math>{{qquad}}{{qquad}}<math>\mathbf{r}-\mathbf{r}'=-R\mathbf{u}_{\rho'}+z\mathbf{u}_z\,</math>{{qquad}}{{qquad}}<math>|\mathbf{r}-\mathbf{r}'|=\sqrt{R2+z^2}</math>{{qquad}}{{qquad}}<math>\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'</math></center> | ||
| + | |||
==Campo en el eje== | ==Campo en el eje== | ||
==Desarrollo multipolar== | ==Desarrollo multipolar== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 21:42 8 ene 2010
Contenido |
1 Enunciado
En el plano XY se encuentra una distribución de carga lineal, formando un anillo, de radio R y con una distribución de carga no uniforme dada, en coordenadas cilíndricas, por
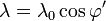
![\varphi'\in(-\pi,\pi]](/wiki/images/math/0/4/4/044ea3bbccb9a391ff5ff855c1f626b0.png)
- Halle el potencial eléctrico producido por el anillo en los puntos del eje Z.
- Calcule el campo eléctrico producido por el anillo en el mismo eje.
- Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo?
2 Potencial en el eje
El potencial en el eje del anillo puede hallarse por integración directa, según la expresión
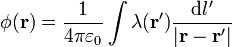
Tenemos que