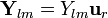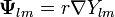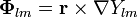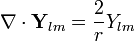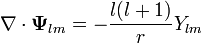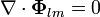Armónicos esféricos vectoriales
De Laplace
(Diferencias entre revisiones)
(→Definición) |
(→Fuentes escalares y vectoriales) |
||
| Línea 10: | Línea 10: | ||
==Fuentes escalares y vectoriales== | ==Fuentes escalares y vectoriales== | ||
| + | A partir de la definición y de las propiedades de los [[armónicos esféricos]] tenemos las siguientes fuentes para los armónicos esféricos vectoriales | ||
| + | |||
| + | ===Fuentes escalares=== | ||
| + | Tomando la divergencia de cada campo | ||
| + | |||
| + | :<math>\nabla\cdot\mathbf{Y}_{lm}=\frac{2}{r}Y_{lm}</math> | ||
| + | |||
| + | :<math>\nabla\cdot\mathbf{\Psi}_{lm}=-\frac{l(l+1)}{r}Y_{lm}</math> | ||
| + | |||
| + | :<math>\nabla\cdot\mathbf{\Phi}_{lm}=0</math> | ||
==Aplicación a la mecánica de fluidos== | ==Aplicación a la mecánica de fluidos== | ||
==Aplicación al electromagnetismo== | ==Aplicación al electromagnetismo== | ||
Revisión de 10:25 24 mar 2008
Contenido |
1 Definición
Los armónicos esféricos vectoriales constituyen una extensión del concepto de armónico esférico a campos vectoriales. Para cada armónico esférico,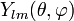 
, se definen tres armónicos esféricos vectoriales
2 Fuentes escalares y vectoriales
A partir de la definición y de las propiedades de los armónicos esféricos tenemos las siguientes fuentes para los armónicos esféricos vectoriales
2.1 Fuentes escalares
Tomando la divergencia de cada campo
