Entrar Página Discusión Historial Go to the site toolbox

Proceso isotermo y adiabático consecutivos

De Laplace

(Diferencias entre revisiones)
(Nueva página: == Enunciado== Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar ...)
Línea 80: Línea 80:
T_3 = T_2\left(\frac{P_2}{P_3}\right)^{\dfrac{1}{\gamma}-1}=
T_3 = T_2\left(\frac{P_2}{P_3}\right)^{\dfrac{1}{\gamma}-1}=
  T_1\left(\frac{2P_1}{P_1}\right)^{\dfrac{1}{\gamma}-1}=
  T_1\left(\frac{2P_1}{P_1}\right)^{\dfrac{1}{\gamma}-1}=
-
2^{\frac{1}{\gamma}-1}T_1
+
\frac{T_1}{2^{1-\frac{1}{\gamma}}}
</math>
</math>
</center>
</center>
 +
En el proceso adiabático se cumple
 +
<center>
 +
<math>
 +
Q_{23}=0
 +
</math>
 +
</center>
 +
La variación de energía interna es
 +
<center>
 +
<math>
 +
\Delta U_{23}=nc_v(T_3-T_2)=\frac{5}{2}nR(T_3-T_1)=
 +
\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)
 +
</math>
 +
</center>
 +
Hemos usado que el aire se puede considerar un gas ideal diatómico, y por
 +
tanto, <math>c_v=5R/2</math>. Al ser adiabático, el trabajo en el proceso es
 +
<center>
 +
<math>
 +
W_{23}=\Delta U_{23}=\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)
 +
</math>
 +
</center>
 +
 +
=== Proceso completo ===
 +
Las cantidades pedidas en el proceso completo son
 +
 +
<center>
 +
<math>
 +
\begin{array}{l}
 +
\Delta U = \Delta U_{12}+\Delta U_{23} =\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)
 +
\\ \\
 +
Q=Q_{12}+Q_{23}=nRT_1\ln 2
 +
\\ \\
 +
W==W_{12}+W_{23}=\Delta U-Q =
 +
\Delta U_{12}+\Delta U_{23} =\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)-nRT_1\ln 2=
 +
-nRT_1\left(\displaystyle \ln 2 +\frac{5}{2}-\frac{5}{2^{2-1/\gamma}}\right)
 +
\end{array}
 +
</math>
 +
</center>
 +
 +
=== Posición del estado 3 en el diagrama <math>PV</math> ===
 +
Vamos a determinar la posición del estado 3 en el diagrama, teniendo en cuenta que <math>\gamma>1</math>.
 +
Tenemos
 +
<center>
 +
<math>
 +
\frac{T_1}{T_3}=2^{1-\frac{1}{\gamma}}=f(\gamma)
 +
</math>
 +
</center>
 +
La función <math>f(\gamma)</math> es monótona creciente en el intervalo
 +
<math>\gamma\in[1,+\infty)</math>, pues
 +
<center>
 +
<math>
 +
\frac{\mathrm{d}f}{\mathrm{d}\gamma}=\frac{2^{1-1/\gamma}}{\gamma^2}\ln2>0
 +
</math>
 +
</center>
 +
en ese intervalo. Además tenemos
 +
<center>
 +
<math>
 +
\begin{array}{lccr}
 +
f(1)=1&&f(\infty)=2
 +
\end{array}
 +
</math>
 +
</center>
 +
Por tanto, se cumple
 +
<center>
 +
<math>
 +
T_3<T_1
 +
</math>
 +
</center>
 +
De una manera similar podemos concluir que
 +
<center>
 +
<math>
 +
V_2<V_3<V_1
 +
</math>
 +
</center>
 +
Esos valores corresponden a la posición del estado 3 que podemos ver en la
 +
representación del proceso en el diagrama <math>PV</math>. La pendiente de la
 +
adiabática es mayor que la de la isoterma, por lo que al expandirse el gas
 +
dejamos la isoterma a la izquierda de la adiabática. Ahora podemos concluir que el
 +
trabajo total realizado por el gas es negativo, pues el área bajo la isoterma es
 +
mayor que el área bajo la adiabática

Revisión de 13:29 24 abr 2009

Contenido

1 Enunciado

Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle

  1. La temperatura final
  2. El trabajo total realizado por el gas
  3. El calor total absorbido por el gas
  4. La variación de energía interna

2 Solución

El gráfico representa los dos procesos a los que se somete el gas, primero una compresión isoterma y después una expansión adiabática. Analicemos cada uno de estos procesos

2.1 Compresión isoterma

Los datos que tenemos de este proceso son

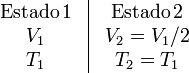
\begin{array}{c|c} \begin{array}{c} \mathrm{Estado\,1}\\V_1\\T_1 \end{array}& \begin{array}{c} \mathrm{Estado\,2}\\V_2=V_1/2\\T_2=T_1 \end{array} \end{array}

Al ser isotermo la variación de energía interna del gas es nula

ΔU12 = 0

El trabajo realizado es

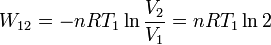
W_{12}=-nRT_1\ln\frac{V_2}{V_1}=nRT_1\ln2

Y el calor absorbido es

Q12 = − W12 = nRT1ln2

2.2 Expansión adiabática

El proceso viene descrito por los parámetros

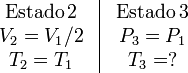
\begin{array}{c|c} \begin{array}{c} \mathrm{Estado\,2}\\ V_2=V_1/2\\ T_2=T_1 \end{array}& \begin{array}{c} \mathrm{Estado\,3}\\ P_3=P_1\\ T_3= ? \end{array} \end{array}

Podemos determinar P2 usando la ley de Boyle para relacionar los estados 1 y 2

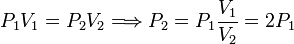
P_1V_1=P_2V_2\Longrightarrow P_2=P_1\frac{V_1}{V_2}=2P_1

Y ahora usamos la ecuación de Poisson para relacionar los estados 2 y 3

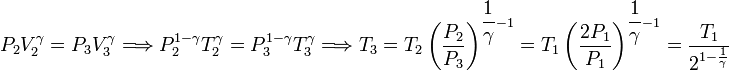
P_2V_2^{\gamma}=P_3V_3^{\gamma}\Longrightarrow P_2^{1-\gamma}T_2^{\gamma}=P_3^{1-\gamma}T_3^{\gamma} \Longrightarrow T_3 = T_2\left(\frac{P_2}{P_3}\right)^{\dfrac{1}{\gamma}-1}= T_1\left(\frac{2P_1}{P_1}\right)^{\dfrac{1}{\gamma}-1}= \frac{T_1}{2^{1-\frac{1}{\gamma}}}

En el proceso adiabático se cumple

Q23 = 0

La variación de energía interna es

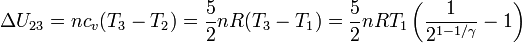
\Delta U_{23}=nc_v(T_3-T_2)=\frac{5}{2}nR(T_3-T_1)= \frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)

Hemos usado que el aire se puede considerar un gas ideal diatómico, y por tanto, cv = 5R / 2. Al ser adiabático, el trabajo en el proceso es

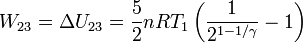
W_{23}=\Delta U_{23}=\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)

2.3 Proceso completo

Las cantidades pedidas en el proceso completo son

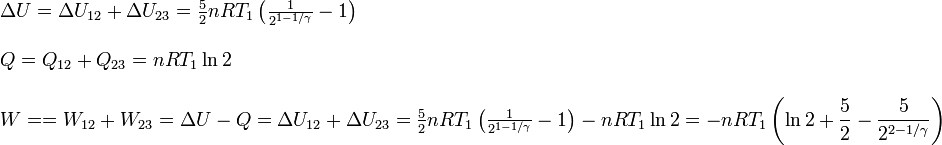
\begin{array}{l} \Delta U = \Delta U_{12}+\Delta U_{23} =\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right) \\ \\ Q=Q_{12}+Q_{23}=nRT_1\ln 2 \\ \\ W==W_{12}+W_{23}=\Delta U-Q = \Delta U_{12}+\Delta U_{23} =\frac{5}{2}nRT_1\left(\frac{1}{2^{1-1/\gamma}}-1\right)-nRT_1\ln 2= -nRT_1\left(\displaystyle \ln 2 +\frac{5}{2}-\frac{5}{2^{2-1/\gamma}}\right) \end{array}

2.4 Posición del estado 3 en el diagrama PV

Vamos a determinar la posición del estado 3 en el diagrama, teniendo en cuenta que γ > 1. Tenemos

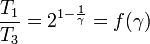
\frac{T_1}{T_3}=2^{1-\frac{1}{\gamma}}=f(\gamma)

La función f(γ) es monótona creciente en el intervalo 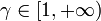\gamma\in[1,+\infty), pues

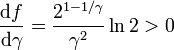
\frac{\mathrm{d}f}{\mathrm{d}\gamma}=\frac{2^{1-1/\gamma}}{\gamma^2}\ln2>0

en ese intervalo. Además tenemos

\begin{array}{lccr} f(1)=1&&f(\infty)=2 \end{array}

Por tanto, se cumple

T3 < T1

De una manera similar podemos concluir que

V2 < V3 < V1

Esos valores corresponden a la posición del estado 3 que podemos ver en la representación del proceso en el diagrama PV. La pendiente de la adiabática es mayor que la de la isoterma, por lo que al expandirse el gas dejamos la isoterma a la izquierda de la adiabática. Ahora podemos concluir que el trabajo total realizado por el gas es negativo, pues el área bajo la isoterma es mayor que el área bajo la adiabática

Obtenido de "http://tesla.us.es/wiki/index.php/Proceso_isotermo_y_adiab%C3%A1tico_consecutivos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace